Pen-Write E-Library

SCHEME OF WORK
WEEKS TOPICS
1. Whole numbers
- Counting and writing in millions, billions and trillions

2. Whole numbers
- Problems solving in quantitative aptitude reasoning using large numbers.

3. Fractions
- Types (proper and improper fractions)

4. Fractions
- Equivalent fractions, concepts of Equivalent fractions in sharing commodities, problems solving in quantitative aptitude.

5. Fractions
- Ordering of fractions, conversion of fractions to percentages and vice-versa, conversion of fractions to decimals and vice-versa.

6. Fractions
- Addition and subtraction

7. Fractions
- Multiplication and division

8. Prime numbers and factors

9. Least common multiple and Highest common factor of whole numbers

10. LCM and HCF
- Problems solving on quantitative aptitude reasoning involving LCM and HCF, the difference between LCM and HCF

11. Estimation
- Estimation of dimensions and distances, on capacity and mass of given objects, problems solving on quantitative reasoning in estimation.

12. Revision

LESSON 1
TOPIC: WHOLE NUMBERS.
CONTENTS:
(i) What whole numbers are.
(ii) Counting numbers
(ii). How to identify figures written in millions, billions and trillions.
(iv). How to translate numbers written in figures to words and vice-versa.

What are whole numbers?
Whole Numbers are also called Integers. There are positive Integers (whole numbers) and negative Integers (whole numbers). Examples of positive integers are 1, 2, 3, 4, 5, etc. , while examples of negative integers are – 1, – 2, – 3, – 4, – 5, etc.

Counting numbers
The figure 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are called digits or units which form counting numbers.
Identification of Large Numbers (reading and writing)
i. Numbers written in thousands must contain at least 4 digits. The four digits must have one comma separating it from the right hand side.
E.g. 1,000; 6,000; 8,912

ii. Numbers written in millions must contain at least 7 digits. The seven digits must have two commas separating them in “threes” from the right hand side.
Examples: 12,000,000 stands for 12 million.
2,000,000 stands for 2 million.
1,000,000 stands for 1 million.
238,000,000 stands for 238 million.

iii. Numbers written in billions must contain at least ten digits with three commas separating them in “threes” from the right hand side.
Examples: 12, 000, 000, 000 stands for 12 billion.
4, 000, 000, 000 stands for 4 billion.
7,456,201,456 stands for 7 billion, four hundred and fifty six million, two hundred and one thousand, four hundred and fifty six.
835, 000, 000, 000 stands for 835 billion.

iv. Numbers written in trillions must contain at least thirteen digits with three commas separating them in “threes” from the right hand side.
Examples: 7,000, 000, 000, 000 stands for 7 trillion.
25, 000, 000, 000, 000 stands for 25 trillion.
714, 000, 000, 000, 000 stands for 714 trillion.
1, 000 million is called a trillion.

v. Translation of numbers written in figures to words and vice-versa

Examples
1. Write the following numbers in words:
(a) 51807508051754
Solution:
51807508051754 = 51, 807, 508, 051, 754 stands for fifty one trillion, eight hundred and seven billion, five hundred and eight million, fifty one thousand, seven hundred and fifty four

(b) 6006006006
Solution:
(c) 6006006006 = 6,006,006,006 stands for six billion, six million, six thousand and six

EVALUATION:
Question 1. Write the following figures in words:
(i). 145238654037 (ii). 78482493861 (iii). 512278374415
(iv). 734015090700018 (v). 89780260044784 .

Question 2. Express the following in figures:
(i). Seven hundred and ninety-eight million, one hundred and thirty- two thousand five
hundred and forty- five.
(ii). Twenty-four billion, seventy-eight million , four hundred and thirty-six thousand , one
hundred and forty -eight.
(iii). Thirteen trillion, nine hundred and forty-one billion, three hundred and twenty-four million,
forty-seven thousand, one hundred and ninety-eight.
(iv). Four hundred and seventeen trillion, two hundred and eighty billion, five hundred and six
thousand, eight hundred and eighteen.
(v). Eighteen million, twenty-five thousand, six hundred and one.

READING ASSIGNMENT:
 TEXT BOOK: New General MATHEMATICS, for Junior Secondary Schools 1 (Upper Basic Edition). Authors: M.F. Macrae, A.O. Kalejaiye, Z. I. Chima, G. U. Garba and others. (Pages 19 – 21).

ASSIGNMENT:
TEXT BOOK: New General MATHEMATICS, for Junior Secondary Schools 1 (Upper Basic Edition). Book – 1 . Answer the questions from (Page 20: Ex. 2a, Q1 – Q5; Ex. 2b, Q1– Q14 and Page 21: Ex. 2c, Q1 & Q2.




LESSON 2
TOPIC: NUMBER SYSTEM
OBJECTIVE: At the end of the lesson, students should be able to count and write whole numbers in millions and billions.

CONTENT:

Number in figures ....Number in words
3 500 320 Three million, five hundred thousand, three hundred and twenty
25 423 508 Twenty-five million, four hundred and twenty three thousand, five hundred and eight
123 020 600 One hundred and twenty three million, twenty thousand and six hundred
1 054 800 003 One billion, fifty-four million, eight hundred thousand and three

EVALUATION:
Write the following in figures
(a) Ten billion, eight hundred and thirty-seven million, two hundred and forty-five thousand, six hundred and eighty two.
(b) Seventy-nine billion, three hundred and sixty-four million, one hundred and eighty one thousand, four hundred and sixty.
Write in words
(c) 8 236 746 517
(d) 532 384 329 348

ASSIGNMENT:
Write in figures:
(a) Nine billion, fifty-four million, six hundred thousand and twelve.
(b) Fifty-seven billion, three hundred and fourteen million, eight hundred and seventy-eight thousand and fourteen.
Write in words:
(c) 65 473 218 239
(d) 740 502 416 824
(e) 91 412 003 675

Convert any number into words


Practice Test




LESSON 3
TOPIC: COUNTING IN BILLIONS AND TRILLIONS
OBJECTIVE: At the end of the lesson, students should be able to:
1. Count in trillions
2. Write in trillions.

CONTENT:
Number in words Number in figures
One million 1 000 000
One billion 1 000 000 000
One trillion (one thousand billion) 1 000 000 000 000

Hint: one thousand billion is called one trillion



EVALUATION:
Write in figures:
(a) Five trillion, seven hundred billion, thirteen million, two hundred and fifty eight thousand, one hundred and twenty.
(b) Sixty-eight trillion, one hundred and five billion, one hundred and forty-five million, three hundred thousand and eighty one.
(c) Ninety-two trillion, four hundred and one.

ASSIGNMENT:
Write in words
(a) 12 008 002 003 040
(b) 95 850 160 055 178
(c) 759 015 040 500 015
(d) 34 127 003 448 123
(e) 36 740 271 062 289

https://youtu.be/BGiYOemaBRc

LESSON 4
TOPIC: ORDERING OF WHOLE NUMBERS
OBJECTIVE: At the end of the lesson, the students should be able to:
1. Arrange large numbers in ascending order of magnitude
2. Arrange large numbers in descending order of magnitude.

CONTENT:
Ascending order: (from smallest to largest)
(a) 104 245 695; 410 245 695; 140 245 695; 41 245 695; 14 245 695
Solution: 14245695; 41 245 695; 104 245 695; 140 245 695; 410 245 695.
(b) Arrange in descending order:
68 205 145 300 681, 68 705 146 300 681, 68 508 746 300 681, 86 105 045 300 681, 681 005 045 300 681.
Solution: 686 005 045 300 681, 86 105 045 300 681, 68 705 146 300 681, 68 508 746 300 681, 68 205 145 300 681.

EVALUATION:
Arrange in ascending order:
(a) 440 655 268, 404 556 268, 414 565 268, 424 740 268
(b) 625 101 464, 526 101 446, 652 101 644, 562 101 964, 562 404 946
Arrange in descending order
(c) 12 984 204 167, 12 974 204 197, 12 814 204, 12 984 240 176.

ASSIGNMENT:
Arrange in descending order:
(a) 84 200 782 148, 894 201 287 041, 948 204 781 141, 498 701 287 824
(b) 948 504 784 141, 498 901 387 834, 378 601 673 200, 787 661 956 883
(c) 3 452 180 205 130, 3 542 480 201 075, 3 425 780 205 730, 3 254 870 120 570

further studies
Further Studies 1

Further Studies 2

practice test
Practice Test





LESSON 5
TOPIC: APPROXIMATION OF LARGE NUMBERS
OBJECTIVE: At the end of the lesson, the students should be able to:
1. Round off numbers to given whole numbers or units required.

CONTENT:
Approximate to the nearest billion:
(a) 3/164 546 000 = 3 000 000 000 or 3 billion
(b) 7 726 300 000 = 8 000 000 000 or 8 billion
(c) Approximate 4 548 729 380 342 → 5 000 000 000 000

EVALUATION:
Round the following off to the nearest billion
(a) 186 500 405 310 168
(b) 870 602 505 784
(c) 271 750 246 571
(d) 628 108 459 257

Correct to the nearest trillion
(a) 7 942 361 428 540
(b) 9 531 456 728 210

ASSIGNMENT:
Round the following off to the nearest trillion:
(a) 69 481 216 824 450
(b) 38 584 652 267 120
(c) 149 614 821 243 504
(d) 89 361 425 682 201
(e) 78 452 366 774 305

view powerpoint presentation
https://drive.google.com/file/d/0Bz3Mh6 ... sp=sharing

practice test
http://www.educationquizzes.com/ks3/mat ... 101005051/




LESSON 6
TOPIC: FACTORS AND MULTIPLES
REFERENCE BOOK: New General Mathematics for JS1, page 23
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to find the factors of a given whole number.
CONTENTS
A factor is a whole number which can divide a larger number exactly without a remainder.
Example, 1, 2, 3, 4 ,6, and 12 are the factors 12.
Find all the factors of 40.
40 = 1 x 40
= 2 x 20
= 4 x 10
= 5 x 8
Factors of 40 are 1,2,4,5,8,10,20 and 40

Example 2
Find all the factors of 210
210 = 1 x 210
= 2 x 105
= 3 x 70
= 5 x 42
= 6 x 35
= 7 x 30
= 10 x 21
Factors of 210 are 1,2,3,5,6,35,42,70,105 and 210

EVALUATION: Find all the factors of:
(a) 45
(b) 30
(c) 180
(d) 240

ASSIGNMENT Find all the factors of:
(a) 48
(b) 144
(c) 360
(d) 105




LESSON 7
TOPIC: MULTIPLES
REFERENCE BOOK: New General Mathematics for JS1, Page 23
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to state the multiples of given numbers.
CONTENTS
Example:
Find 5 multiples of 6
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
Multiples of 6 are 6, 12, 18, 24 and 30

Example 2
List 5 multiples of 15
15 x 1 = 15
15 x 2 = 30
15 x 3 = 45
15 x 4 = 60
15 x 5 = 75
Multiples of 15 are: 15, 30, 45, 60 and 75

EVALUATION: Write down 5 multiples of each of the following:
(a) 13
(b) 9
(c) 21
(d) 19
(e) 30

ASSIGNMENT Write down 5 multiples of each of the following:
(a) 12
(b) 10
(c) 50
(d) 42

https://youtu.be/0NvLtTwnUHs





LESSON 8
TOPIC: Prime Numbers and Prime Factors
REFERENCE BOOK: New General Mathematics f or JS 1, Page 24
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express numbers as product of their prime factors.
CONTENTS
A prime number is a number which has only two different factors, itself and 1.
Example of prime factors are 2, 3, 5, 7…
A prime factor of a number is a factor which is a prime number.
E g 2 and 7 are prime factors of 28

Example 1
Express 60 as a product of its prime factors
60 = 2 x 2 x 3 x 5

Example 2
Express 81 as product of its prime factors
81 = 3 x 3 x 3 x 3

Example 3
Express 144 as product of its prime factors
144 = 2 x 2 x 2 x 2 x 3 x 3

EVALUATION:
(a) Which of the following are prime numbers?
23, 27, 29, 61, 55, 19, 47, 31, 17
(b) Express 240 as product of its prime factors
(c) Express 360 as product of its prime factors

ASSIGNMENT
Express each of each the following as product of its prime factors
(a) 90
(b) 270
(c) 540

https://youtu.be/XGbOiYhHY2c







LESSON 9
TOPIC: LCM and HCF
REFERENCE BOOK: New General Mathematics for Js1, Page 27
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to :
(1) Find the lcm of given numbers
(2) Find the HCF of given numbers

CONTENTS
Example
Find the LCM of 8, 9 and 12
8 = 2 x 2 x 2
9 = 3 x 3
12 = 2 x 2 x 3
The LCM of 8, 9 and 12 are 2 x 2 x 2 x 3 x 3

Example 2
Find the LCM of 24, 28, 36 and 50
24 = 2 x 2 x 2 x3
28 = 2 x 2 x 7
36 = 2 x 2 x 3 x 3
50 = 2 x 5 x 5
The LCM of 24, 28, 36 and 50 is 2 x 2 x 2 x 3 x 3 x 5 x 7
= 12600

HIGHEST COMMON FACTOR
Example
Find the HCF of 2 x 3 x 3 x 5; 2 x 2 x 3 x 3 x 3; 3 x 3 x 5 x 7
HCF is 3 x 3 = 9

EVALUATION
Find the LCM of the following:
(a) 9, 6 and 5
(b) 18, 27 and 35
Find the HCF of the following:
(a) 144, 216 and 360
(b) 63, 42 and 21

ASSIGNMENT
Find the LCM and the HCF of the following:
(a) 9, 12 and 15
(b) 10, 16 and 18
(c) 280, 105 and 175
(d) 288, 180 and 108

https://youtu.be/wLUBEOOQqb8

LESSON 10
TOPIC: WHOLE NUMBERS (QUANTITATIVE APTITUDE REASONING)
CONTENTS:
Problems solving in quantitative aptitude reasoning using large numbers
Sample1:
Study these examples and use them to answer the given questions.
(81:9) (100:10) (144:12)
(5:25) (8:64) (13:169)
(a) (7:49) (10:100) (11:?)
Here first numbers in a bracket are squared to have the second number.
(11: ? ) = (11: 121)
(b) (490000: 700) (1210000: ?)
Here the square root of the first numbers in a bracket gives second number.
(1210000: ?) = (1210000: 1100)
Evaluation:
Now do the following:
1. (12300 : 151290000) (45600 : ?)
2. (10000 : 100000000) (200000 : ?)
3. (9000 : 30) (?:250)

https://drive.google.com/file/d/0B8CPo8 ... sp=sharing





LESSON 11
TOPIC: FRACTIONS 1
CONTENTS:
(i). What are fractions?
(ii). Types of fraction.
(iii). Equivalent fractions

What are fractions?
Fractions are portion or part of whole number that describes quantities. Examples
Consider the shapes below:



Types of fraction
Fractions are divided into four basic types:
(i). A Proper Fraction – It is a fraction having both numerator and denominator. And such is said to be rational. In a proper fraction, its numerator is smaller in quantity than its denominator. We can use a funny example to explain. Suppose a 15 years old boy is made to carry on his head two small tubers of yam. We can see that he can comfortably and conveniently carry them without feeling the heaviness of the weight of the tubers, on his neck. If we let the boy be the denominator and the two tubers of yam to be numerator, we can reason or compare that the numerator (the yam tubers) and the 15 year-old boy (the denominator) are not equal in weight. Obviously in this example the numerator is lighter than the denominator. It is a proper thing for anyone to do when placing loads on a child’s head. The load on a child’s head should not be heavier than the body mass of that child. So, it is proper. That is exactly what a proper fraction looks like.
Examples of proper fractions are : etc.

(ii). An Improper Fraction – It is also a fraction having both numerator and denominator. But for an improper fraction its numerator is bigger in quantity than its denominator. Using our funny example above, we will believe that it is not proper for a seven-year old boy to carry a whole drum of petrol upon his head. It will be improper to do that. So, an improper fraction has its numerator larger in quantity than its denominator.
Examples of improper fractions are : etc.

(iii). A mixed Fraction – It is a fraction having two parts merged together. One part is a whole number while the other part is purely a proper fraction. Therefore, a mixed fraction is a joining of both a whole number and a proper fraction. As an example 4 2/5 is a mixed fraction, containing 4 as a whole number and 2/5 as proper fraction. Other examples of mixed fractions are etc.

(iv). A decimal Fraction – It is simply another language or another word for a decimal number. i.e. a number having a decimal point present in it. A decimal number (decimal fraction) is opposed to a vulgar fraction. A vulgar fraction is a fraction having both a numerator and a denominator. The word vulgar simply means common or familiar. Both the proper and the improper fractions can be called as vulgar fractions, because both types have numerators and denominators. Another name for vulgar fraction is common fraction. Examples of Decimal Fractions are: 9.45 , 9.4558976 , 0.0003287 , 8.91234 , 9.00674 , 0.1 , 0.01432 , etc.

EVALUATION:
1. What do you understand by word ‘fractions’?
2. List or mention 4 types of fractions and give 2 examples of each.
3. State the difference between ‘vulgar’ and ‘decimal’ fractions.





LESSON 12
Equivalent fractions.
CONTENTS:
(i). When are fractions said to be equivalent?
(ii). Test of Equivalent Fractions.
(iii). Writing Equivalent Fractions.
(iv). Reducing Equivalent Fractions to their lowest forms.
(v). Using equivalent fractions to share commodities (Word Problems).


ALITERNATIVELY: Each of the fractions can be reduced to its lowest term. If the lowest terms are equal to each other or to one another after the reduction, then it shows the equivalence. However, if after reduction the results are not the same, it then means the fractions are not equivalent.


Writing Equivalent Fractions.


Reducing Equivalent Fractions to their lowest forms.

EVALUATION:
1. Show that 37/47 and 481/611 are equivalent fractions.
2. Show that 7/21 and 13/39 are equivalent fractions.
3. Reduce 99/264 to its simplest / lowest form.
4. Reduce 63/231 to its simplest / lowest form.
5. Copy and complete the following: (a). 3/7=/56 . (b). 6/15=/180 .

Using equivalent fractions to share commodities (Word Problems).
Worked Examples:
1. A woman shares 30 apples between her two daughters. The first child got 6/10 of all the apples. How
many apples did she get? and how many did the other daughter get?
Solution :
Total number of apples = 30. Fraction of apples to the first child = 3/5 .
Number of apples = 3/5 ×30=18 apples. The first daughter shares 18 apples.
The second child gets 4/10 of the total number of apples. This is equivalent to 2/5 .
The second child gets 2/5 × 30=12 apples.
The first child gets 18 apples while the second gets 12 apples.


2. Three quarters of the eggs in a basket are good. If the total number of eggs in the basket is 60,
how many eggs in the basket are bad?
Solution :
Total number of eggs = 60.
Number of good eggs = 3/4×60=45 eggs.
Hence, number of bad eggs = Total number of eggs – Number of good eggs.
= 60 – 45 = 15 eggs.



EVALUATION:
1. There are 420 students in a school. 1/3 of the population is made up of girls.
(a). How many boys are in the school ?
(b). How many girls are in the school?
(c). Express the number of boys as a fraction of all the students.
(d). Express the number of girls as a fraction of all the students.

2. Three water tanks with volumes 81 liters, 243 liters and 405 liters were filled with 27 liters, 81 liters and 135 liters respectively. Express their water contents as fractions of their capacity.

READING ASSIGNMENT:
NEW GENERAL MATHEMATICS: Pages 29 – 39 for Junior secondary Schools 1. (UBE Edition ).

ASSIGNMENT:
(NEW GENERAL MATHEMATICS, for Junior secondary Schools Book – 1. (UBE Edition )
(i). Page 30 ; Ex. 4a 1. Attempt Questions g - l. ; 4a 2. Attempt Questions g - l
(ii). Page 31 ; Ex. 4b. Attempt Question 4 1-3 only .
(iii). Page 31-32 ; Ex. 4c. 1 (a-f), 2a and 3b Attempt Questions 13 and 17 only.

https://youtu.be/CA9XLJpQp3c

LESSON 13
TOPIC: FRACTIONS.
Content:
Problems solving in quantitative aptitude reasoning on equivalent fractions








LESSON 14
TOPIC: FRACTIONS 3.
CONTENTS:
(i). Ordering of fractions.
(ii). Conversion of fractions to percentages
(iii). Conversion of percentages to fractions.
(iv). Conversion of fractions to decimals.
(v). Conversion of decimals to fractions.

Ordering of fractions.
Ordering of fractions simply means arranging the fractions either from the least to the greatest or greatest to least. In other words, we arrange the fractions in ascending or descending order. To do this, we find the L.C.M (Least Common Multiple) of the denominators of the fractions we intend to order. In other words we find the equivalent fraction of each of the given fractions so that each equivalent fraction is having its denominator equal to the common L.C.M.

Examples:
1: Arrange the following fractions in ascending order 3/4 , 2/( 3) , 1/(6 ) , 1/2 .
Solution:
Since the L.C.M = 12 , we write:
3/4 as (3 × 3)/(4 × 3) = 9/12 .

2/3 as (2 × 4)/(3 × 4) = 8/12 .

1/6 as (1 × 2)/(6 × 2) = 2/12 .

1/2 as (1 × 6)/(2 × 6) = 6/12 .

We now compare the four results and order them accordingly. Ascending order we have the array as:
2/12 , 6/12 , 8/12 , 9/12 . ∴ the required ordering is : 1/6 , 1/2 , 2/3 , 3/4 .
Arrange these fractions in descending order 3/4 , 1/2 , 4/5 and 7/10 .



ALTERNATIVE METHOD:
The L.C.M of 4 , 2 , 5 and 10 = 20.
Add the four fractions as follows: 3/4 + 1/2 + 4/5 + 7/10 = (5(3)+10(1)+4(4)+2(7))/20 = (15+10+16+14)/20 .
This is same as 15/20 + 10/20+16/20+14/20 . This shows that 3/4 = 15/20 , 1/2=10/20 , 4/5 = 16/20 , and 7/10= 14/20 .
Hence the ordering of 3/4 , 1/2 , 4/5 and 7/10 in descending order is 16/20 , 15/( 20) , 14/20 , 10/20 ; which are
4/5 , 3/4 , 7/10 , 1/2 respectively.



EVALUATION:
1. Arrange the following fractions in descending order:
(i). 1/4 , 2/( 5) , 3/10 , ( 3)/5 . (ii). 2/3 , 1/4 , 3/9 , 7/12 . (iii). 5/6 , 7/12 , 5/18 , 1/2 . (iv). 4/5 , 1/3 , 7/15 , 23/30 .
2. Arrange the above sets of fractions (i - iv) in ascending order.

Conversion of fractions to percentage.

Examples :
Express 2/15 as percentage.
Solution:
There are two possible ways to answer the question.
METHOD – 1: Write 2/15 as 2/15×100 = 200/15 =13 1/3%.
2/15 = 13 1/3% in percentage.
METHOD – 2: Write 2/15 as (2⁄3)/(15⁄3) = (2⁄3)/5 = (2/3 ×20)/(5×20) = (40⁄3)/100 = (13 1/3)/100
2/15 = 13 1/3% in percentage also



Conversion of percentages to fractions.
Examples:
Express 65% as fraction.
Solution:
Write 65% as 65% = 65/100 = 13/20 . 65% = 13/20 .
Express 24% as fraction .
Solution:
Write 24% as 24% = 24/100 = 6/25 . ∴ 24% = 6/25 .
Express 0.35% as fraction.
Solution:
Write 0.35% as 0.35% = (0.35)/100 = (0.35 × 100)/(100 × 100) = 35/10000 = 7/2000 .

EVALUATION:
Express each of the following fractions as percentage.
5/8 , 17/20 , 9/25 , 1/90 .
Express each of the following percentages as fraction.
64% , 45 % , 0.125 % , 0.17 % .







LESSON 15
Conversion of fractions to decimals:
There are two methods of doing this conversion. There is the general method which can be used any time and on any type of vulgar fraction; and there is another method when the denominator of the fraction contains power/powers of ten. In this second case the given fraction can first be converted to an equivalent fraction.

Examples:
Convert the following common fractions to decimal fractions (decimal numbers).
2/5 , 3/4 , 144/225 .
Solutions:
First, we can use the equivalent fractions method, before the general method.
Write 2/5 as 2/5 = (2 × 2)/(5 × 2) = 4/10 = 0.4 2/5 = 0.4
Write 3/4 as 3/4 = (3 × 25)/(4 × 25) = 75/100 = 0.75 ∴ 3/4 = 0.75
Write 144/225 as 144/225 = (144 × 4)/(225 × 4) = 576/1000 = 0.576 ∴ 144/225 = 0.576



Second, the general method (for all condition) is used when the denominator of the given fraction does not contain power(s) of 10. This is by dividing the numerator by the denominator mentally or through long-division previously learnt by students in their Primary School days.
NOTE: Teachers to demonstrate this approach to students as an alternative method.

Conversion of decimals to fractions.
Examples:
Convert 0.65 to a common or a vulgar fraction.
Solution:
To do this we simply multiply the given decimal fraction by 100 and at the same time divide it by 100.
Write 0.65 as 0.65 = (0.65 × 100)/100 . If we carefully notice the expression we will see that what we are doing
in essence is just multiplying 0.65 by unity (1). Because 100/100= 1.
⇒ (0.65 × 100)/100 = 65/100 = 13/20 , ( when further reduced to the lowest term ). ∴ 0.65 = 13/20 .
Convert 0.6 to a common or a vulgar fraction.
Solution:
To do this we simply multiply the given decimal fraction by 10 and at the same time divide it by 10.
Write 0.6 as 0.6 = (0.6 × 10)/10 = 6/10 = 3/5 . ⇒ ∴ 0.6 = 3/5 .
Convert 0.125 to a common fraction.
Solution:
To do this we multiply the given decimal fraction by 1000 and at the same time divide it by 1000 , to have 0.125 = (0.125 × 1000)/1000 = 125/1000 = 25/200 = 5/40 = 1/8 , ( when fully simplified to its lowest form ).

EVALUATION:
Change the following common / vulgar fractions to decimal fractions.
9/15 , 1/19 , 2/23 , 17/3 , 123/341 .
2. Change the following decimal fractions to the vulgar or common fractions.
0.56 , 0.0015 , 5.35 , 0.222 , 1.98



READING ASSIGNMENT:
TEXT BOOK: NEW GENERAL MATHEMATICS for Junior Secondary Schools 1(UBE Edition). Pages 78 – 80.

https://youtu.be/CA9XLJpQp3c

ASSIGNMENT:
TEXT BOOK: NEW GENERAL MATHEMATICS for Junior Secondary Schools 1(UBE Edition).
Page78, Ex. 9h: Attempt Q1 to Q40; Page 79, Ex. 9j: Q15 to Q30; Page 79: Ex. 9k: Q1 and Q2.
Page 80, Ex 9l: Attempt Q2 to Q10.

LESSON 16
TOPIC: Fractions – Addition and Subtraction.
CONTENTS of the TOPIC :
(i). Addition of Vulgar fractions.
(ii). Subtraction of Vulgar fractions.
(iii). Addition of Decimal fractions.
(iv). Subtraction of Decimal fractions.
(v). Word problems on Addition and Subtraction of fractions.
(vi). Word Problems involving Addition and Subtraction of decimal fractions.

CONTENTS’ DEVELOPMENT
(i). Addition of Vulgar fractions.
Examples:
Question – 1: Add the fractions 2/3 and 4/5 .
Solution:
2/3 + 4/5 = (5×2 +3×4)/15 = (10+12)/15 = 22/15 = 17/15 .
Question – 2: Add the fractions 4 3/11 , 7 1/3 .
Solution: 4 3/11+7 1/3 = 47/11+ 22/3 = (47(3)+11(22))/33 = (141+242)/33 = 383/33 = 1120/33 ( in mixed fraction).
( Note: In this method, we first change the mixed fractions to Improper fractions before adding ).



(ii). Subtraction of Vulgar fractions.
Question – 1: Subtract 2 3/4 from 5 3/5 .
Solution: 5 3/5 - 2 3/4 = 28/5-11/4 = (4(28)-5(11))/20 = (112-55)/20 = 57/20 = 2 17/20 .

EVALUATION:
Question – 1: Add the fractions 2/13 and 3/5 .
Question – 2: Subtract 4 1/4 from 7 1/3 .
Question – 3: Obtain the sum of 1 2/5 and 3 1/4 , subtract 2 1/3 .








LESSON 17
CONTENTS’ DEVELOPMENT
(iii). Addition of Decimal fractions.
Example:
Question – 1: What is the sum of 21.52, 42.68, 146.5 and 12.27 ?



(iv). Subtraction of Decimal fractions.
Example:
Question – 1: Find the positive difference between 128 and 69.126

(v). Word problems on Addition and Subtraction of fractions.
Examples:
Question – 1: A tailor needs 1 1/3 m cloth and he cuts this length from a cloth of 2 1/4 m long.
what fraction remains?
Solution: = (2 1/4 - 1 1/3) = 9/4-4/3 = (3(9)-4(4))/12 = (27-16)/12 = 11/12 .

Question – 2: A house wife went to the market for shopping, she spent two-seventh of her money on
food stuffs and one-quarter on clothing materials. What fraction of her money remains?
Solution: Total amount spent = 2/7+1/4 = (8+7)/28 = (15 )/28 . ∴ What is left is 1 – 15/28 = 13/28 .



EVALUATION:
Question – 1: Obtain the sum of 0.00914 , 72.013 and 681.08, without use of calculator.
Question – 2: Subtract 67.09 from 85.921 , without use of calculator.
Question – 3: What number is 9 2/5 more than 7 1/2 ?
Question – 4: A man spent 11/15 of his salary on transport, feeding and health. He then saves 1/5 of the salary.
What fraction of his salary remains?







LESSON 18
CONTENTS’ DEVELOPMENT
(vi). Word Problems involving Addition and Subtraction of decimal fractions.
Examples:
Question – 1: How many liters of petrol will a car owner buy to fill his tank of 65.125 liters if he already
has 56 liters in his tank?
Solution: He needs 65.125 – 56.000 more liters to fill his tank.
= 9.125 liters.
Question 2: Find the length of the third wire if the total length of the three wires is 825.4m and the lengths of
the remaining 2 wires are 321.56m and 239.548m.
Solution: 825.4-( 321.56+239.548 )=825.4-561.108 = 264.292 meters.

EVALUATION:
Question – 1: A boy has N1,856.80. He likes and wants to buy a shirt costing N 2,100.00. What
amount does he need before he can buy the shirt of his choice?
Question – 2: Obtain the perimeter of a shape with sides 14.8cm, 37 cm and 25.4cm.
Question –3: A trader went to market with N 5680.00. She bought articles worth N 4, 325.78. How
much has she left to buy other things?
Question – 4: A man withdrew N 11,400 from his accounts for shopping, his son came back from school
and demanded a sum of N 2,650 as what he had to pay in school. So, the man went back to
withdraw this amount for the son. What was the total the man withdrew? If the total
amount he had in that bank before withdrawal was N 45,117.79, how much did he have
left after the two withdrawals?
READING ASSIGNMENT:
TEXT BOOK: MAN MATHEMATICS – 1, for Junior Secondary Schools (3RD Edition). Pages 28 – 42.

https://youtu.be/5juto2ze8Lg

ASSIGNMENT:
TEXT BOOK: MAN MATHEMATICS – 1, for Junior Secondary Schools ( 3RD Edition ).Ex. D4. (Page 38). Attempt Questions 5 , 6 , 9 , 10 , 13 , 16 and 17.

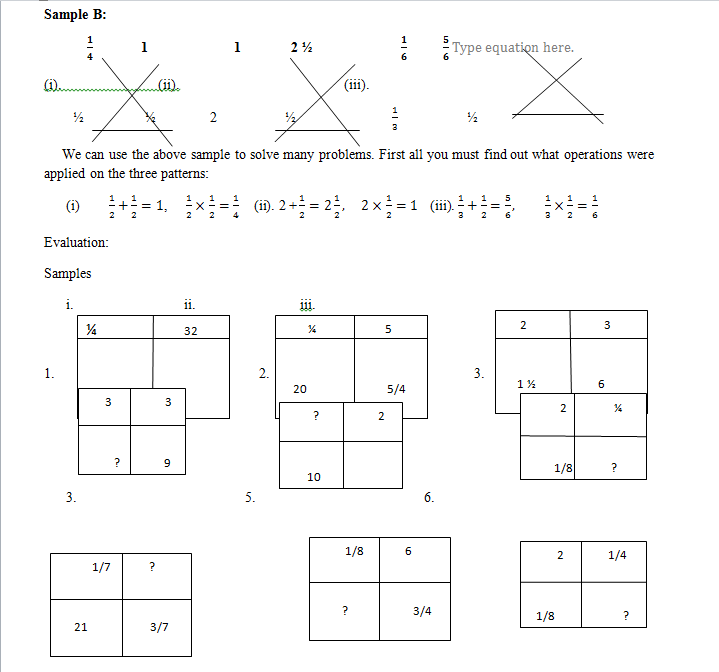
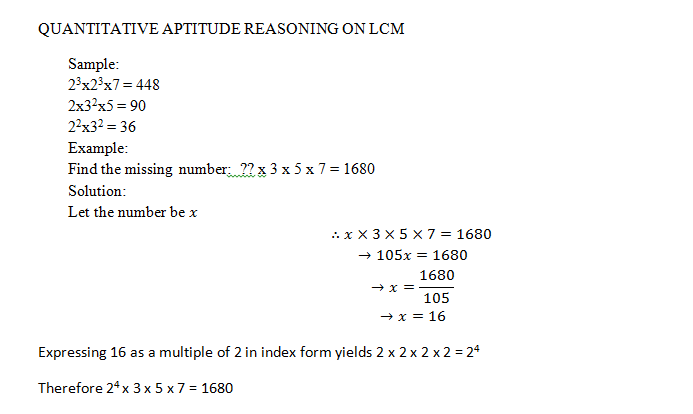TOPIC: FACTORS, PRIME NUMBERS, LEAST COMMON MULTIPLES (LCM) & HIGHEST COMMON FACTORS (HCF) OF INTEGERS.
CONTENTS:
(i). Definition of Factors; and the Relationship between Factors and Multiples.
(ii). Meaning and examples of Prime Numbers.
(iii). Difference between Factors and Prime Factors.
(iv). Expressing Numbers as product of Prime Factors.
(v). Common factors and the Highest Common Factor (H.C.F) of two, three or more numbers
(vi). Least Common Multiple (L.C.M) of Numbers.


LESSON 19
DEFINITION OF FACTORS AND MULTIPLES & THEIR RELATIONSHIP
FACTORS: When two or more smaller numbers multiply to give a bigger number, these smaller numbers are called factors of the bigger number. In another sense we can say a factor is a number which can divide another number exactly without any remainder.
Examples:
The factors of 24 are 1 , 2 , 3, 4 , 6 , 8 , 12 , and 24.
The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
The factors of 50 are 1, 2, 5, 10, 25 and 50.

MULTIPLES: This is the product of numbers (factors) that gives other numbers.
Thus, 24 is: a multiple of 1 twenty-four times.
a multiple of 2 twelve times.
a multiple of 3 eight times.
a multiple of 4 six times.
a multiple of 6 four times.
a multiple of 8 three times.
a multiple of 12 two times.
a multiple of 24 (itself) once.
This shows the relationship between Factors and Multiples.
NOTE: The Teacher can make students do same analysis (orally) for 60 and 50 as has just been done for 24 above.

MEANING AND EXAMPLES OF PRIME NUMBERS.
A prime number is a whole number which is divisible only by itself and 1. In other words, a whole
Number that has no other factor(s) except 1 and the number itself is referred to as a Prime Number.
Number 1 or Integer 1 is not considered as a Prime Number.
Examples of Prime Numbers:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97. ( as those prime numbers between 1 and 100 ).

EVALUATION:
Question – 1: List the factors of (a). 48 . (b). 64 . (c). 105 .
Question – 2: 48 , 64 , 108 are multiples of which numbers?
Question –3: Define a Prime Number and list all the Prime Numbers between 200 and 300.




LESSON 20
DIFFERENCE BETWEEN FACTORS AND PRIME FACTORS
The factors of 24 are 1 , 2 , 3, 4 , 6 , 8 , 12 , and 24. However, those factors that are Prime among all these are only 2 and 3. Hence, the Prime Factors of 24 are 2 and 3 only.

The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60. However, those factors that are Prime among all these are only 2 , 3 and 5. Hence, the Prime Factors of 60 are 2 , 3 and 5 only.
The factors of 50 are 1, 2, 5, 10, 25 and 50. However, those factors which are Prime among all these are only 2 and 5. Hence, the Prime Factors of 50 are 2 and 5 only.

EXPRESSING NUMBERS AS PRODUCT OF PRIME FACTORS.
Examples:
Express 200 as product of prime factors in index form.
Solution:
200 = 4 ×50 =2 ×2 ×25=2×2 ×5 ×5= 2^2×5^2
Express 180 as product of prime factors in index form.
Solution:
2×90=2×2 ×45=2×2×3×15=2×2×3×3×5=2^2×3^2×5.
Express 510 as product of prime factors in index form.
Solution:
2×255=2×3×85=2×3×5×17 .



EVALUATION:
Question – 1: List the factors of 250 and the Prime factors of 250.
Question – 2: List the factors and prime factors of 180.
Question – 3: Express 252 as product of prime factors in index form.
Question – 4: Express 440 as product of prime factors in index form.
Question – 4: Express 15288 as product of prime factors in index form.





LESSON 21
COMMON FACTORS AND HIGHEST COMMON FACTOR (H.C.F) OF TWO, THREE OR MORE NUMBERS.
Worked Examples:
Find the Common factors of 42 and 70.
Solution:
The factors of 42 are 1, 2 , 3 , 6, 7 , 14 , 21, 42.
The factors of 70 are 1, 2, 5, 7, 10, 14, 35, 70.
The factors that are common to both numbers or which are found in the two lists are : 1, 2, 7 , 14.
The highest of the common factors here is 14. Hence, the Highest Common Factor ( H.C.F ) of 42 and 70 = 14.

Find the Common factors of 18 and 27. What is their Highest Common Factor?.
Solution:
The factors of 18 are 1, 2 , 3 , 6, 9 , 18.
The factors of 27 are 1, 3, 7, 27.
Their Common Factors are : 1, 3 , 9. Thus, their Highest Common Factor ( H.C. F ) is 9.

Find the Common Factors of 18, 27 and 36. What is their Highest Common Factor?.
Solution:
The factors of 18 are 1, 2 , 3 , 6, 9 , 18.
The factors of 27 are 1, 3, 7, 27.
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36.
Their Common Factors are : 1, 3. Thus, their Highest Common Factor ( H.C. F ) is 3.

LEAST COMMON MULTIPLE (L.C.M) OF NUMBERS.
Worked Examples:
Find the Least Common Multiple ( LCM ) of 42 and 70.
Solution:
Write 42 as product of prime numbers as follows:
42 = 2×21=2×3×7.
Write 70 as product of prime numbers as follows:
70 = 2×35=2×5×7.
Notice those numbers common to both set of prime numbers. The common numbers are 2 and 7.
The Product of 2 and 7 gives 14. Thus, in another way and by the way 14 is the Highest Common Factor
(H.C.F). But the L.C.M (Lowest Common Multiple) = 2×7×3×5=21×10=210.
Therefore the L. C. M of 42 and 70 = 210.

Find the Least Common Multiple ( LCM ) of 18, 27 and 36.
Solution:
Write 18 = 2×9=2×3×3=2×3^2
Write 27 = 3×9=3×3×3=3^3.
Write 36 = 2×18=2×2×9=2×2×3×3=2^2×3^2.
In this example, the numbers to be picked for L.C.M are 3^3× 2^2.
Therefore the Least Common Multiple of 18, 27 and 36 = 3^3× 2^2=27×4=108.



EVALUATION:
Find the Common Factors of 60 and 84. State the Highest Common Factor.
What is the Lowest Common Multiple of (L.C. M) of 60 and 84 ?.
Find the L.C.M and H.C.F of 42, 90 and 105.





LESSON 22
QUANTITATIVE APTITUDE REASONING ON LCM
Sample:
23x23x7 = 448
2x32x5 = 90
22x32 = 36
Example:
Find the missing number: ?? x 3 x 5 x 7 = 1680
Solution:
Let the number be x
∴x×3×5×7=1680
→105x=1680
→x=1680/105
→x=16
Expressing 16 as a multiple of 2 in index form yields 2 x 2 x 2 x 2 = 24
Therefore 24 x 3 x 5 x 7 = 1680



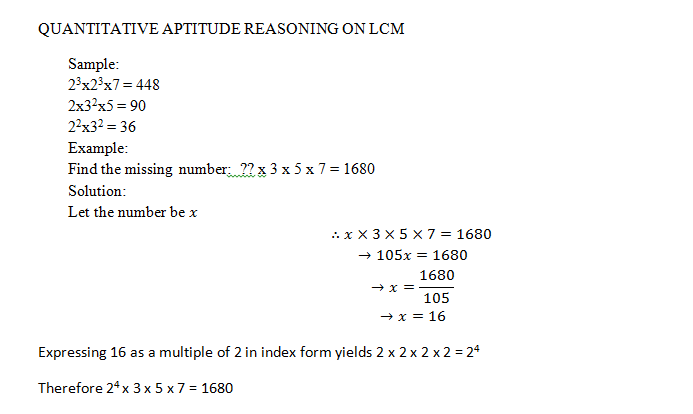
Evaluation
Do the following:







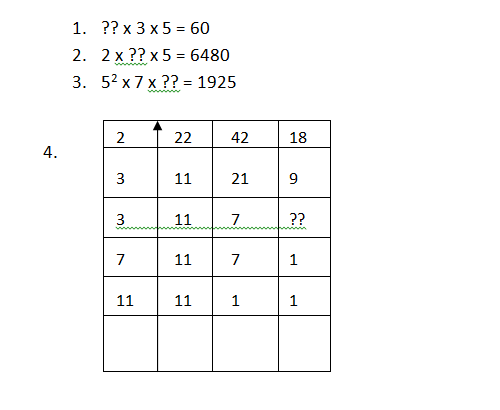LESSON 23
QUANTITATIVE APTITUDE REASONING ON HCF
Sample:
(a). 28 = 2 x 2 x 7 = 22 x 7 (b). 36 = 2 x 2 x 3 x 3 = 22 x 32 (c). 24 = 2 x 2 x 2 x 3 = 23 x 3
Example: Find the missing number in 64 = x6
Solution:
64 =x×x×x×x×x×x
Multiply 2 by it-self in 6 times gives 64.
∴ the missing number is 2 . This implies 64 = 26

EVALUATION
Now do the following by supplying the missing number in each case:
84 = ?? x 2 x 3 x 7
?? = 2 x 3 x 5
?? = 32 x 52



READING ASSIGNMENT:
TEXT BOOK: NEW GENERAL MATHEMATICS for Junior Secondary Schools 1(Upper Basic Edition). Pages 23 – 27).

https://youtu.be/-RhdzNYfF-M

ASSIGNMENT:
TEXT BOOK: NEW GENERAL MATHEMATICS for Junior Secondary Schools 1(Upper Basic Edition). Pages 23 – 27).
Ex. 3c. (Page 24). Attempt Q1 to Q16.
Ex. 3d. (Page 25). Attempt Q1 to Q4.
Ex. 3f. (Page 26). Attempt Q1 to Q4.
Ex. 3h. (Page 27). Attempt Q1 to Q12.
Ex. 3f. (Page 27). Attempt Q1 to Q4.

LESSON 24
TOPIC: APPROXIMATION 1
CONTENTS:
(i). Approximating values of addition and subtraction
(ii). Approximating values of multiplication and division.

APPROXIMATING VALUES OF MULTIPLICATION AND DIVISION.
In approximating a value, one needs to have a rough idea of the answer to calculation prior to the actual calculation.

Examples:
Estimate the values of each following:
43 + 62 + 59 ii. 3.1 + 4.8 + 4.1 iii. Add up 18 and 19
iv. 53 – 38 v. 841 – 392

Solutions:
Actual calculation is 43 + 62 + 59 = 164
Approximation is 40 + 60 + 60 = 160
Actual calculation is 3.1 + 4.8 + 4.1 = 12
Approximation is 3.0 + 5.0 + 4.0 = 12
Actual calculation is 18 + 19 = 37
Approximation is 20 + 20 = 40
Actual calculation is 53 – 38 = 15
Approximation is 50 – 40 = 20
Actual calculation is 841 – 392 = 449
Approximation is 840 – 390 = 450

APPROXIMATING VALUES OF MULTIPLICATION AND DIVISION
Examples
Multiply 63 by 47 ii. 17.32 x 1.07 iii. 703 divided by 21

Solutions:
Multiply 63 by 47
Actual calculation is 63 x 47
That is
63
X 47
441
+ 2520
2961
Approximation is 63 x 47 ≅60 x 50 = 3000
17.32 x 1.07

Solution:
Actual calculation: 17 . 32
1 . 07
121.24
000.00
173.200
18.5324
Approximation is 17.32 x 1.07 ≅17.0 x 1.0 = 17.0

https://youtu.be/FJ5qLWP3Fqo

Evaluation
Calculate and approximate the following:
16.7 + 1.09 ii. 12.48 ÷7.8 iii. 0.333 x 0.667 iv. 7.55 – 3.45



READING ASSIGNMENT:
TEXT BOOK: NEW GENERAL MATHEMATICS for Junior Secondary Schools 1. (UBE Edition). Pages 179 – 182.

https://youtu.be/Mst8iZjIpFE

ASSIGNMENT:
TEXT BOOK: NEW GENERAL MATHEMATICS for Junior Secondary Schools 1. (UBE Edition).
Ex. 23e. (Page 180 - 181). Attempt Q1 to Q3
Ex. 23f. (Page 181). Attempt Q1 to Q10
Ex. 23f. (Page 181). Attempt Q1 to Q10

https://youtu.be/kwh4SD1ToFc