SCHEME OF WORK
WEEK TOPIC
1. Revision of First Term Work.
2. Simple Equations: Harder problems on Algebraic Fractions.
3. Word Problems on algebraic Fractions. World problem leading to Simple Algebraic Fractions.
4. Linear inequality in one variable. Graphical representations of solutions of linear inequalities in one variable.
5. Graphs: plotting points on the Cartesian plane (the axis and plotting of points). Linear Equation in two variables – plotting the graph of Linear Equations in two variables
6. More work on plotting and joining points to form plane shapes on Cartesian Planes.
7. Graphs: Linear graphs from real life situations - plotting linear graphs from real life situation. Quantitative reasoning – solving quantitative aptitude problems.
8. Plane Figures/shapes: Revision on properties of parallelogram rhombus and kite.
9. Scale drawing – Drawing to scale to represent given distances. Solving problems on quantitative aptitude related to plane shapes/ figures
10. Revision
2ND TERM
WEEK 1
LESSON 1
TOPIC: SIMPLE EQUATION AND WORLD PROBLEMS
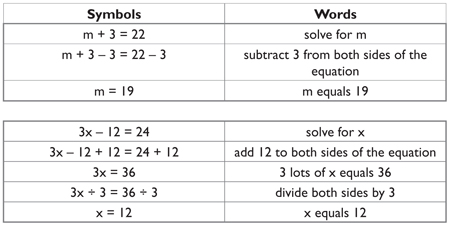
DEFINITION OF EQUATIONS
Equations are open sentences which have the equal sign. Solving an equation means finding a value of the unknown which makes the equation true. Any letter a, f, c, x etc. can be used as unknown. The set of values which make an equation true is called the truth set.
Example 1
Solve the following simple equations:
3a-8 = 10
10x – 7 = 27
4 + 5y = 19
Solution
a.) 3a – 8 = 10
Method 1
3a – 8 + 8 =10 +8
3a = 18
3a/3=18/3 = 6
Method 2
3a – 8 = 10
3a = 10 + 8
3a = 18
a = 18/3 = 6

Note: If a number is moved from one side to an equation over the equal sign to the other side, the sign of the number changes.
b.) 10x – 7 = 27
Method 1
10x – 7 + 7 = 27 + 7
10x = 34
10x/10=34/10
x = 3.4
Method 2
10x – 7 = 27
10x = 27+ 7
x = 34/10 = 3.4
EXAMPLE 2
Solve the following equations:
4(3y-2) = 6
2 (x-8) = 3(x+5)
Solution
4 (3y-2) = 6
Removing the bracket we have
12y-8=6
Solving the equation
12y= 6 +8 =14
y= 14/12 = 7/6 = 1 1/6
2(x-8) = 3(x+5)
Removing the brackets
2x-16 = 3x+15
Collecting the like terms together and solving
-16-15 = 3x-2x
-31 = x
Or
x = -31

EXAMPLE 3
Solve the following equations
(a-2)/3=4
5=(2x-3)/7
2/3x+2/2=1/x
Solution
(a-2)/3=4
Multiply both sides by 3
(a-2)/3 ×3=4×3
a-2 = 12
a =12+2
a = 14
5=(2x-3)/7
Multiply both sides by 7
5×7=2x-3
35 + 3 = 2x
38 =2x
x=38/2
x =19
2/3x+2/2=1/x
Collecting the like terms together
2/3x-1/x=(-1)/x
(L.C.M of 3 and x is 3x)
(2-3)/3x=(-1)/2
(-1)/3x=(-1)/2
-2 = 13x
(-2)/(-3)=x ∴x=2/3
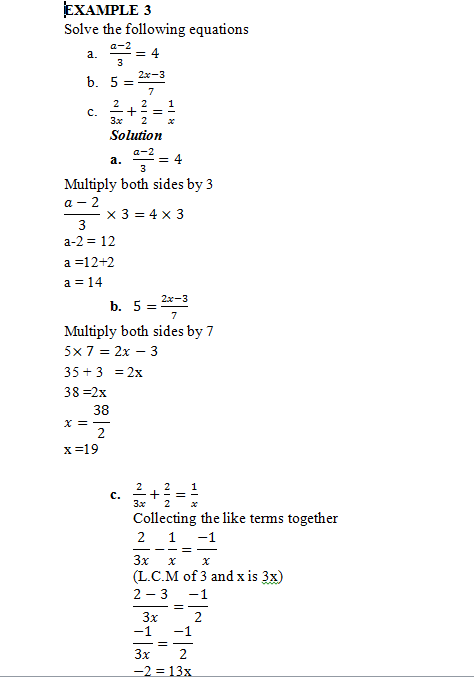
LESSON 2
WORD PROBLEM ON SIMPLE EQUATIONS
This is the same as solving simple equations.
EXAMPLE:
I think of a number, add 3 to it and then divide the result by 5. If the answer equals the original number, what is the number?
The average cost of a number of erasers is 50k. if all the erasers cost N 20, find the total number of erasers.
Solution:
Let the number be x.
3 added to the number becomes: x+3
Divide the result by 5: (x+3)/5
And since the result equals original number, we have,
(x+3)/5=x
Solving, we have,
(x+3)/5=x
(x+3)/5×5/1=x×5
x +3 = 5x
3 = 5x-x
3 = 4x
3/4 = x
Let the number of erasers be y
Average cost of erasers = N20/y
Average cost of erasers = 50/100= 20/y
(50×100)/100=20/y×100
50 = 2000/y
50y = 2000/y×y/1
50y = 2000
∴ y = 40 erasers
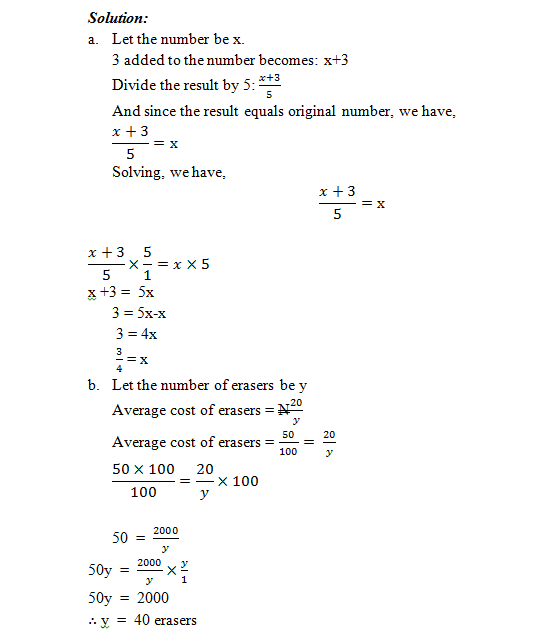
EVALUATION:
Solve the following equations;
4x/5-2x/3=4
(y-3)/3-y/2=0
1=(b-1)/2+(2b+1)/3
https://youtu.be/DfbQjiSooOo
ASSIGNMENT:
Solve x/3-x/4=1
(4x-3)/9-x/3=5(x-1)/6
A sportswoman has a body of mass of xkg. Her mass is i4kg less than that of her friend. If their total mass is 76kg. Find the mass of each of them.
A girl has 12 sweets. She eats n out of them. Find how many sweets she has left if n=2
READING ASSIGNMENT:
New General Mathematics for Junior Secondary Schools 2 by M. F. Macrae et al
LESSON 3
TOPIC: Word Problems. (Changing written information into algebraic form)
REFERENCE BOOK New General Mathematics for JS2, Page 114.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to change written information into algebraic form.

CONTENTS
Change the following into algebraic form:
(a) a number x is doubled: = x + x = 2x
(b) a number n is multiplied by 8 = 8n
(c) a number m is multiplied by 6 and then 4 is added. = 6m + 4
(d) a number y is doubled and then 5 is subtracted. = 2y - 5
(e) a number is 3 less than a = a - 3
EVALUATION: New General Mathematics for JS2, Page 114, Ex 13e, Questions f - j.
https://youtu.be/-ldmqIBHNo0
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2, Page 114, Questions 2a - d.
further studies
Study More...
Study More...
Study More...
practice test
Practice More...
watch video
http://www.youtube.com/watch?v=Y9fpSKkIbHE
LESSON 4
TOPIC: Forming equation from words.
REFERENCE BOOK: New General Mathematics f or JS2, Page 114.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to use the balance method to solve equations.
CONTENTS
Example: I think of a number. I multiply it by 5. I add 15. The result is 100. What is the number I thought of?
Let the number be n
I multiply n by 5: 5n
I add 15: 5n + 15
The result is 100: 5n + 15 = 100
Subtract 15 from both sides.
5n + 15 - 15 = 100 - 15
5n = 85
Divide both sides by 5
5n/5 = 85/5
n = 17.
https://youtu.be/OMjfPxhbf-0
EVALUATION: This lesson is evaluated from New General Mathematics for JS2, Page 114, Ex 13f, Questions 1 - 3.
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2, Page 115, Questions 5, 6 and 8
further studies
Study More...
Study More...
watch video
https://youtu.be/uy9QPLCj-hw
LESSON 5
TOPIC: Word Problems With Brackets.
REFERENCE BOOK: New General Mathematics for JS2, Page 115.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve equations containing brackets.


CONTENTS
I subtract 3 from a certain number, multiply the result by 5 and then add 9. If the final result is 54, find the original number.
Let the number be x
I subtract 3: x - 3
I multiply by 5: 5(x - 3)
I add 9: 5(x- 3) + 9
The result is 54:
5(x - 3) + 9 = 54
= 5x - 15 + 9 = 54
5x = 54 +15 -9
5x = 60
X = 12.
https://youtu.be/2oc29NTWG24
EVALUATION: New General Mathematics for JS2, Page 116, Ex 13g, Questions 1 and 2.
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2, Page 116, Questions 3 and 6.
further studies
Study More...
LESSON 6
TOPIC: Word Problems With Brackets.
REFERENCE BOOK: New General Mathematics f or JS2, Page115.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve equations containing brackets.

CONTENTS
Find two consecutive even numbers such that seven times the smaller number subtracted from nine times the greater number makes 46.
1, 2, 3, 4, 5 . . . are consecutive whole numbers.
2, 4, 6, 8, 10 . . . are consecutive even numbers.
1, 3, 5, 7, 9 . . . are consecutive odd numbers.
Let the number be x and (x + 2)
Multiply x by 7: = 7x
Multiply (x + 2) by 9: = 9(x + 2)
Subtract: 9(x + 2) - 7x
Thus: 9(x + 2) - 7x = 46
9x + 18 - 7x = 46
9x - 7x = 46 - 18
2x = 28
X = 14
The numbers are 14 and 16.
EVALUATION: The lesson is evaluated from New General Mathematics for JS2, Page 116, Ex 13g, Questions 3.
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2: Questions 4 and 7.
further studies
Study More...
practice test
Practice More...
http://www.youtube.com/watch?v=p_ViHA70Gi4
LESSON 7
TOPIC: Word Problems with Fractions
REFERENCE BOOK: New General Mathematics for JS2, Page 117.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve word problems with fractions.

CONTENTS
I add 55 to a certain number and then divide the sum by 3. The result is four times the first number . Find the number.
Let the number be n.
I add 55 to n: this gives n + 55
I divide the sum by 3: this gives (n + 55)/ 3
The result is 4n.
So (n + 55)/3 = 4n
Multiply both sides by 3.
Thus n + 55 = 12n
55 = 12n - n
55 = 11n
55/11 = n
5 = n
https://youtu.be/MMLCiLNkEww
EVALUATION: New General Mathematics for JS2, Page 117, Ex 13h, Questions 1 and 2.
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2: Page 117, Ex 13h, Questions 3, 4 and 11.
further studies
Study More...
practice test
More Practice...
TOPIC: SIMPLE EQUATION AND WORLD PROBLEMS
DEFINITION OF EQUATIONS
Equations are open sentences which have the equal sign. Solving an equation means finding a value of the unknown which makes the equation true. Any letter a, f, c, x etc. can be used as unknown. The set of values which make an equation true is called the truth set.
Example 1
Solve the following simple equations:
3a-8 = 10
10x – 7 = 27
4 + 5y = 19
Solution
a.) 3a – 8 = 10
Method 1
3a – 8 + 8 =10 +8
3a = 18
3a/3=18/3 = 6
Method 2
3a – 8 = 10
3a = 10 + 8
3a = 18
a = 18/3 = 6

Note: If a number is moved from one side to an equation over the equal sign to the other side, the sign of the number changes.
b.) 10x – 7 = 27
Method 1
10x – 7 + 7 = 27 + 7
10x = 34
10x/10=34/10
x = 3.4
Method 2
10x – 7 = 27
10x = 27+ 7
x = 34/10 = 3.4
EXAMPLE 2
Solve the following equations:
4(3y-2) = 6
2 (x-8) = 3(x+5)
Solution
4 (3y-2) = 6
Removing the bracket we have
12y-8=6
Solving the equation
12y= 6 +8 =14
y= 14/12 = 7/6 = 1 1/6
2(x-8) = 3(x+5)
Removing the brackets
2x-16 = 3x+15
Collecting the like terms together and solving
-16-15 = 3x-2x
-31 = x
Or
x = -31

EXAMPLE 3
Solve the following equations
(a-2)/3=4
5=(2x-3)/7
2/3x+2/2=1/x
Solution
(a-2)/3=4
Multiply both sides by 3
(a-2)/3 ×3=4×3
a-2 = 12
a =12+2
a = 14
5=(2x-3)/7
Multiply both sides by 7
5×7=2x-3
35 + 3 = 2x
38 =2x
x=38/2
x =19
2/3x+2/2=1/x
Collecting the like terms together
2/3x-1/x=(-1)/x
(L.C.M of 3 and x is 3x)
(2-3)/3x=(-1)/2
(-1)/3x=(-1)/2
-2 = 13x
(-2)/(-3)=x ∴x=2/3
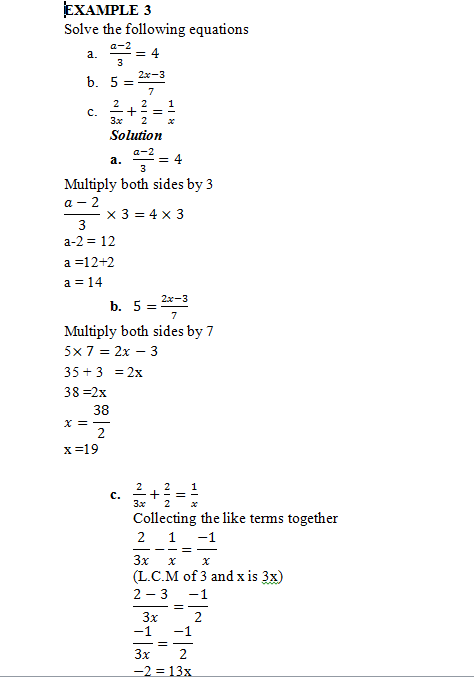
LESSON 2
WORD PROBLEM ON SIMPLE EQUATIONS
This is the same as solving simple equations.
EXAMPLE:
I think of a number, add 3 to it and then divide the result by 5. If the answer equals the original number, what is the number?
The average cost of a number of erasers is 50k. if all the erasers cost N 20, find the total number of erasers.
Solution:
Let the number be x.
3 added to the number becomes: x+3
Divide the result by 5: (x+3)/5
And since the result equals original number, we have,
(x+3)/5=x
Solving, we have,
(x+3)/5=x
(x+3)/5×5/1=x×5
x +3 = 5x
3 = 5x-x
3 = 4x
3/4 = x
Let the number of erasers be y
Average cost of erasers = N20/y
Average cost of erasers = 50/100= 20/y
(50×100)/100=20/y×100
50 = 2000/y
50y = 2000/y×y/1
50y = 2000
∴ y = 40 erasers
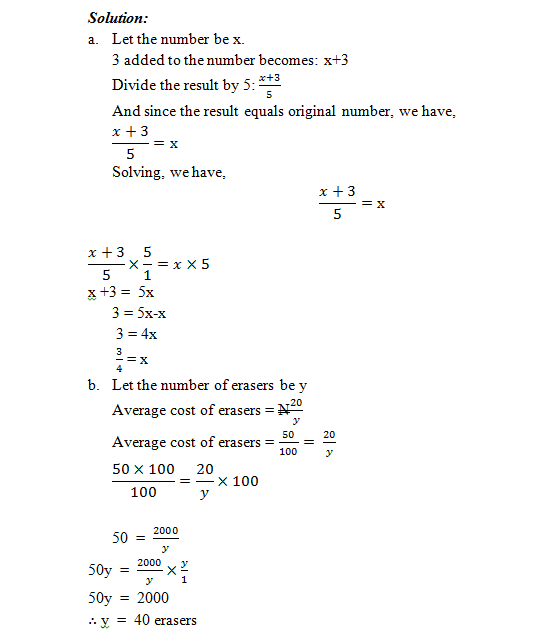
EVALUATION:
Solve the following equations;
4x/5-2x/3=4
(y-3)/3-y/2=0
1=(b-1)/2+(2b+1)/3
https://youtu.be/DfbQjiSooOo
ASSIGNMENT:
Solve x/3-x/4=1
(4x-3)/9-x/3=5(x-1)/6
A sportswoman has a body of mass of xkg. Her mass is i4kg less than that of her friend. If their total mass is 76kg. Find the mass of each of them.
A girl has 12 sweets. She eats n out of them. Find how many sweets she has left if n=2
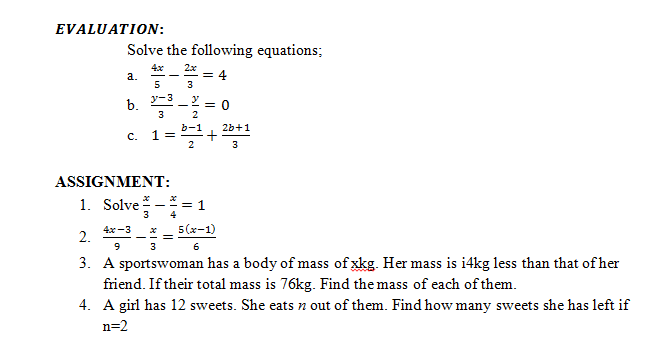
READING ASSIGNMENT:
New General Mathematics for Junior Secondary Schools 2 by M. F. Macrae et al
LESSON 3
TOPIC: Word Problems. (Changing written information into algebraic form)
REFERENCE BOOK New General Mathematics for JS2, Page 114.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to change written information into algebraic form.

CONTENTS
Change the following into algebraic form:
(a) a number x is doubled: = x + x = 2x
(b) a number n is multiplied by 8 = 8n
(c) a number m is multiplied by 6 and then 4 is added. = 6m + 4
(d) a number y is doubled and then 5 is subtracted. = 2y - 5
(e) a number is 3 less than a = a - 3
EVALUATION: New General Mathematics for JS2, Page 114, Ex 13e, Questions f - j.
https://youtu.be/-ldmqIBHNo0
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2, Page 114, Questions 2a - d.
further studies
Study More...
Study More...
Study More...
practice test
Practice More...
watch video
http://www.youtube.com/watch?v=Y9fpSKkIbHE
LESSON 4
TOPIC: Forming equation from words.
REFERENCE BOOK: New General Mathematics f or JS2, Page 114.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to use the balance method to solve equations.

CONTENTS
Example: I think of a number. I multiply it by 5. I add 15. The result is 100. What is the number I thought of?
Let the number be n
I multiply n by 5: 5n
I add 15: 5n + 15
The result is 100: 5n + 15 = 100
Subtract 15 from both sides.
5n + 15 - 15 = 100 - 15
5n = 85
Divide both sides by 5
5n/5 = 85/5
n = 17.

https://youtu.be/OMjfPxhbf-0
EVALUATION: This lesson is evaluated from New General Mathematics for JS2, Page 114, Ex 13f, Questions 1 - 3.
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2, Page 115, Questions 5, 6 and 8
further studies
Study More...
Study More...
watch video
https://youtu.be/uy9QPLCj-hw
LESSON 5
TOPIC: Word Problems With Brackets.
REFERENCE BOOK: New General Mathematics for JS2, Page 115.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve equations containing brackets.


CONTENTS
I subtract 3 from a certain number, multiply the result by 5 and then add 9. If the final result is 54, find the original number.
Let the number be x
I subtract 3: x - 3
I multiply by 5: 5(x - 3)
I add 9: 5(x- 3) + 9
The result is 54:
5(x - 3) + 9 = 54
= 5x - 15 + 9 = 54
5x = 54 +15 -9
5x = 60
X = 12.

https://youtu.be/2oc29NTWG24
EVALUATION: New General Mathematics for JS2, Page 116, Ex 13g, Questions 1 and 2.
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2, Page 116, Questions 3 and 6.
further studies
Study More...
LESSON 6
TOPIC: Word Problems With Brackets.
REFERENCE BOOK: New General Mathematics f or JS2, Page115.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve equations containing brackets.

CONTENTS
Find two consecutive even numbers such that seven times the smaller number subtracted from nine times the greater number makes 46.
1, 2, 3, 4, 5 . . . are consecutive whole numbers.
2, 4, 6, 8, 10 . . . are consecutive even numbers.
1, 3, 5, 7, 9 . . . are consecutive odd numbers.
Let the number be x and (x + 2)
Multiply x by 7: = 7x
Multiply (x + 2) by 9: = 9(x + 2)
Subtract: 9(x + 2) - 7x
Thus: 9(x + 2) - 7x = 46
9x + 18 - 7x = 46
9x - 7x = 46 - 18
2x = 28
X = 14
The numbers are 14 and 16.
EVALUATION: The lesson is evaluated from New General Mathematics for JS2, Page 116, Ex 13g, Questions 3.
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2: Questions 4 and 7.
further studies
Study More...
practice test
Practice More...
http://www.youtube.com/watch?v=p_ViHA70Gi4
LESSON 7
TOPIC: Word Problems with Fractions
REFERENCE BOOK: New General Mathematics for JS2, Page 117.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve word problems with fractions.

CONTENTS
I add 55 to a certain number and then divide the sum by 3. The result is four times the first number . Find the number.
Let the number be n.
I add 55 to n: this gives n + 55
I divide the sum by 3: this gives (n + 55)/ 3
The result is 4n.
So (n + 55)/3 = 4n
Multiply both sides by 3.
Thus n + 55 = 12n
55 = 12n - n
55 = 11n
55/11 = n
5 = n
https://youtu.be/MMLCiLNkEww
EVALUATION: New General Mathematics for JS2, Page 117, Ex 13h, Questions 1 and 2.
ASSIGNMENT: Answer the following questions from New General Mathematics for JS2: Page 117, Ex 13h, Questions 3, 4 and 11.
further studies
Study More...
practice test
More Practice...
WEEK 2
LESSON 8
TOPIC: WORD PROBLEMS ON ALGEBRAIC FRACTIONS
CONTENT:
Word problems leading to simple algebraic fractions
Problem solving
WORD PROBLEMS LEADING TO SIMPLE ALGEBRAIC FRACTIONS
When solving word problems, the following points are important:
Use a letter to represent the unknown
Translate problem from words to algebraic form
Make an equation out of it
Solve equation completely to get the unknown
Where it involve fraction, first clear the fraction using LCM
Give the answer in a written form
Check the result against the information given in the question
https://youtu.be/DfbQjiSooOo
PROBLEM SOLVING
Ojo add 15 to a number and then divide the sum by three. The result is twice the first number. Find the number.
Solution:
Let the number be n
Ojo add 15 to n : n+15
Ojo divide the result by 3: (n+15)/3
The result is 2n
This implies that: (n+15)/3=2n
Multiply both sides 3 to clear the fraction
n+15=6n
Collecting like terms,
15=6n-n
15=5n
Dividing both side by 5, the result is 3 ie n=3
Therefore, the number is 3
I add 60 to a certain number and then divide the result by 12, the quotient is 6. Find the original number.
Solution:
Let the number be x
I add 60 to the number i.e x+60
Dividing result by 12 implies (x+60)/12
Quotient means answer ∴(x+60)/12=6
Multiply through by 12 to clear the fraction: x+60=6x12
This implies: x+60=72
x=72-60=12
The original number is 12.
Juliet is n years old and her brother is half of her age. The sum of their ages is half of their father’s age who is now 60. How old is Juliet and her brother?

Solution:
Juliet age is n years
Her brother’s age is half of hers i.e 1/2 n years
Their Father’s age is 60 years and half of 60 is 30.
Sum of their ages is half of their father:
n+1/2 n=30
Multiply through by 2 to clear the fraction:
2n+n=60
3n=60
n=60/3=10
This means that: Juliet is 10 years and her brother is 5 years.
https://youtu.be/QIbJR_TD9Vk
Evaluation:
Find a number such that when 20 is added to ¼ of it, the result is 1 1/7 times the original number.
One-fifth of an even number added tone-sixth of the next even number makes a total of 15. Find the two numbers. (Hint: let the numbers be n and n+2).
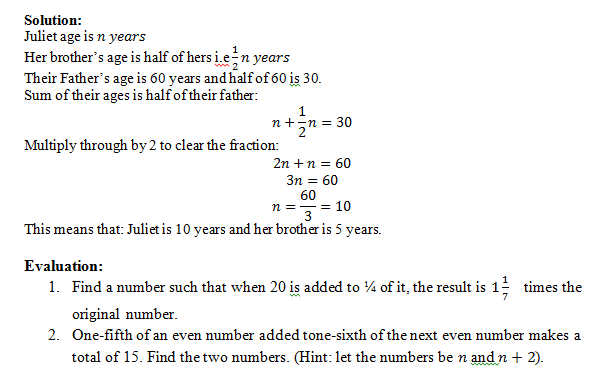
Reading
Assignment:
New General Mathematics JSS-2 UBE Edition. Page 114 to 117.
New General Mathematics JSS-2 UBE Edition. Ex. 13h: Attempt Q1 to Q16 Page 117 to 118.
TOPIC: WORD PROBLEMS ON ALGEBRAIC FRACTIONS
CONTENT:
Word problems leading to simple algebraic fractions
Problem solving
WORD PROBLEMS LEADING TO SIMPLE ALGEBRAIC FRACTIONS
When solving word problems, the following points are important:
Use a letter to represent the unknown
Translate problem from words to algebraic form
Make an equation out of it
Solve equation completely to get the unknown
Where it involve fraction, first clear the fraction using LCM
Give the answer in a written form
Check the result against the information given in the question
https://youtu.be/DfbQjiSooOo
PROBLEM SOLVING
Ojo add 15 to a number and then divide the sum by three. The result is twice the first number. Find the number.
Solution:
Let the number be n
Ojo add 15 to n : n+15
Ojo divide the result by 3: (n+15)/3
The result is 2n
This implies that: (n+15)/3=2n
Multiply both sides 3 to clear the fraction
n+15=6n
Collecting like terms,
15=6n-n
15=5n
Dividing both side by 5, the result is 3 ie n=3
Therefore, the number is 3
I add 60 to a certain number and then divide the result by 12, the quotient is 6. Find the original number.
Solution:
Let the number be x
I add 60 to the number i.e x+60
Dividing result by 12 implies (x+60)/12
Quotient means answer ∴(x+60)/12=6
Multiply through by 12 to clear the fraction: x+60=6x12
This implies: x+60=72
x=72-60=12
The original number is 12.
Juliet is n years old and her brother is half of her age. The sum of their ages is half of their father’s age who is now 60. How old is Juliet and her brother?

Solution:
Juliet age is n years
Her brother’s age is half of hers i.e 1/2 n years
Their Father’s age is 60 years and half of 60 is 30.
Sum of their ages is half of their father:
n+1/2 n=30
Multiply through by 2 to clear the fraction:
2n+n=60
3n=60
n=60/3=10
This means that: Juliet is 10 years and her brother is 5 years.
https://youtu.be/QIbJR_TD9Vk
Evaluation:
Find a number such that when 20 is added to ¼ of it, the result is 1 1/7 times the original number.
One-fifth of an even number added tone-sixth of the next even number makes a total of 15. Find the two numbers. (Hint: let the numbers be n and n+2).
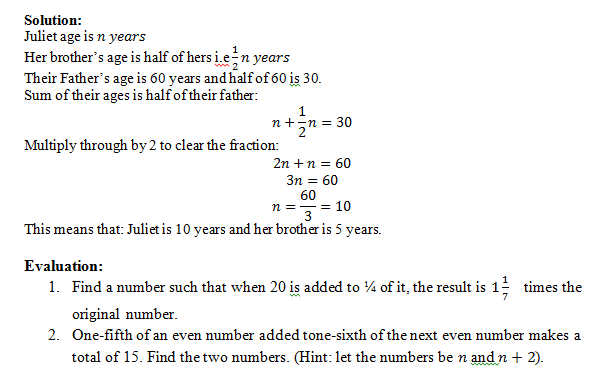
Reading
Assignment:
New General Mathematics JSS-2 UBE Edition. Page 114 to 117.
New General Mathematics JSS-2 UBE Edition. Ex. 13h: Attempt Q1 to Q16 Page 117 to 118.
WEEK 3
LESSON 9
TOPIC Inequalities
REFERENCE BOOK Macmillan Progressive Mathematics for JS1,Page 69
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to :
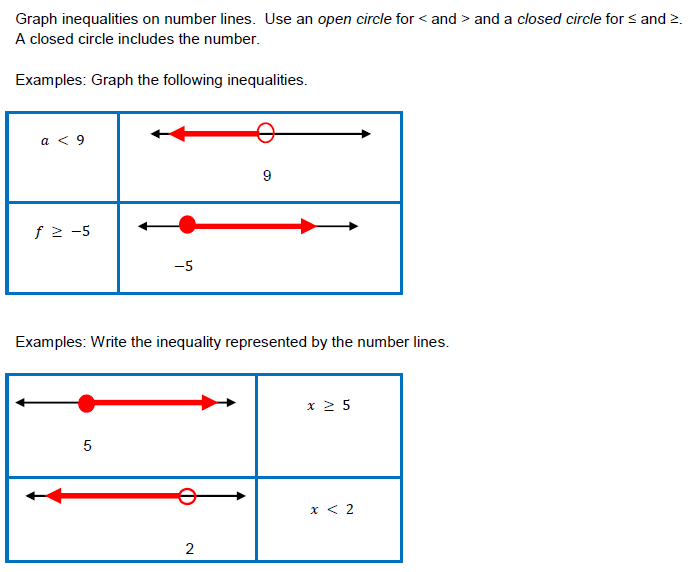
(1) Use the inequality symbols ≥ , ≤, ≠, and ≠ correctly.
(2) Write and interpret linear inequality in one variable.
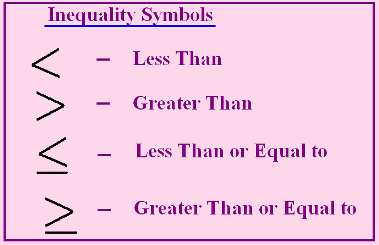
CONTENTS
≤ less than or equal to
≥ greater than or equal to
≠ not equal to
5 + 5 ≠ 7
3 + 6 ≥ 8
40 ≤ 94
Write the appropriate symbols in the boxes.
(a) 3 is less than 7 □
(b) 6 + 8 is greater than 10 □
(c) 41 is not equal to 33 □
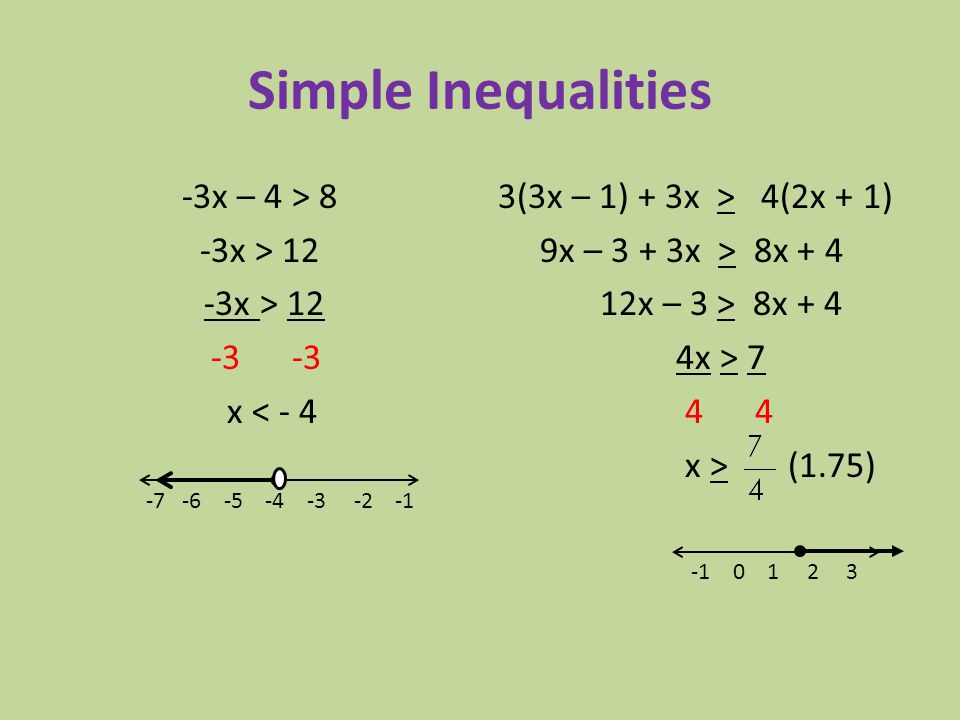
EVALUATION This lesson is evaluated from New General Mathematics for JS2 Page 209, ex. 22a , questions 2a - j.
https://youtu.be/wcBwdz-ZBaM
ASSIGNMENT New General Mathematics for JS2, Page 210, ex. 22a, Questions 7a - i
Study More...
practice test
Quiz 1
Quiz 2
Quiz 3
LESSON 10
TOPIC Graphs of inequalities
REFERENCE BOOK Macmillan Progressive Mathematics forJS2, Page 74
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to show the graphs of linear inequalities in one variable on the number line.

CONTENTS
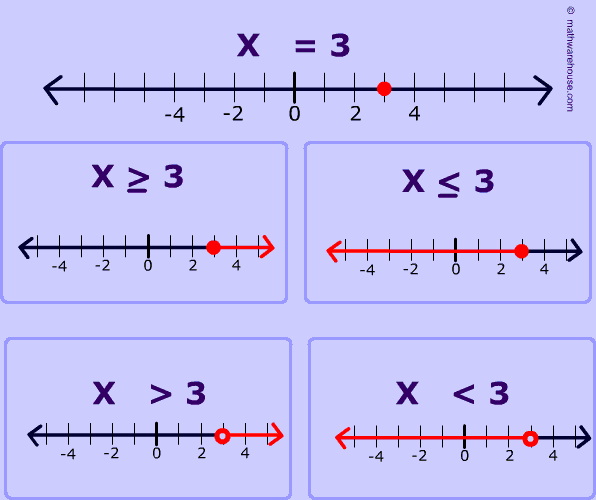
x ≤ 2
-3 -2 -1 0 +1 +2 +3
(a)
-1 0 +1 +2 +3 +4 x ≥ 0
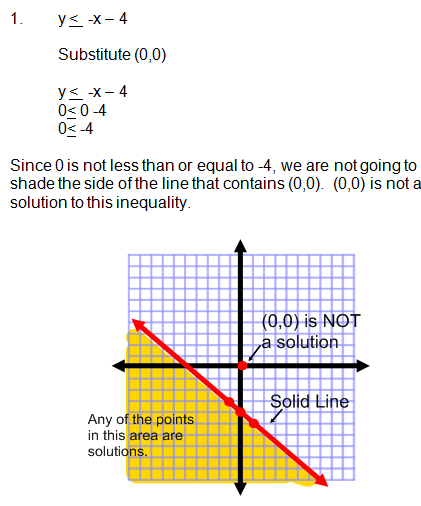
EVALUATION The lesson is evaluated from New General Mathematics for JS2, Page 212, Ex 22d Questions a - e
ASSIGNMENT New General Mathematics for JS2 PAGE 212, Ex 22d, Questions 2a - e
further studies
Study More...
Study More...
practice test
Practice More...
Practice More...
view slide show
https://docs.google.com/presentation/d/ ... sp=sharing
https://www.youtube.com/watch?v=AjZzACaeIco
LESSON 11
TOPIC Solution of inequalities (Balance method)
REFERENCE BOOK Macmillan Progressive Mathematics for JS2 Page 70.
BEHAVIOURAL OBJECTIVE: At the end of this lesson, students should be able to solve linear inequalities in one variable.
CONTENTS
EXAMPLE: (a). Solve the inequality: x + 4 ≤ 6
Subtract 4 from both sides.
X + 4 - 4 ≤ 6 - 4
X ≤ 2
(b). Solve 6 ≤ 2x - 1 and show your answer on a graph.
6 ≤ 2x - 1
Add 1 to both sides
7≤ 2x
7/2 ≤ x
3.5 ≤ x or x≥ 3.5

https://youtu.be/97-HZQabPvc
EVALUATION The lesson is evaluated from New General Mathematics for JS2 Page 213 Ex 22e questions 1- 5.
ASSIGNMENT New General Mathematics for JS2 Page 213, Ex 22e questions 6 - 9
further studies
Study More...
http://www.youtube.com/watch?v=UeQeHF7gojU
LESSON 12
TOPIC MULTIPLICATION AND DIVISION BY NEGATIVE NUMBERS
REFERENCE BOOK Macmillan Progressive Mathematics for JS2 Page 76.
BEHAVIOURAL OBJECTIVE: At the end of this lesson, students should be able to solve inequalities involving multiplication and division by negative numbers.

CONTENTS
(a) Solve 5 - x ≥ 3
Subtract 5 from both sides
5 - 5 - x ≥ 3 -5
- X ≥ -2
Multiply both sides -1 and reverse the inequality
i e x ≤ 2
Page 215 Ex 22g Questions 1-5
ASSIGNMENT New General Mathematics for JS2, Page 214 Ex 22g, Questions 6-9.
further studies
Study More...
Study More...
practice test
Practice More...
watch video
https://youtu.be/I6Njd2XWF5E
LESSON 13
TOPIC Solving word problems involving inequalities.
REFERENCE BOOK Macmillan Progressive Mathematics for JS2 , Page 69.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve word problems on inequalities.

CONTENTS

(a) If 7 is subtracted from a certain number, the result is less than 15. Find the values of the number.
Solution: Let y represent the number.
Y - 7 ≤ 15
Y ≤ 15 + 7
Y ≤ 22

EVALUATION: The lesson is evaluated from New General Mathematics for JS2 Page 215, Ex 22h, Questions 1- 5
http://www.youtube.com/watch?v=iMKv6jOYut0
ASSIGNMENT: New General Mathematics for JS2 Page 215, Questions 6 - 9.
further studies
Study More...
LESSON 14
TOPIC: LINEAR INEQUALITIES
CONTENT:
Inequalities
Graphs of inequalities
Solution of inequalities
INEQUALITIES
In mathematics, we use the equal s sign, = , to show that quantities are the same. How ever, very often, quantities are different, or unequal. The inequalities symbols are as follows:
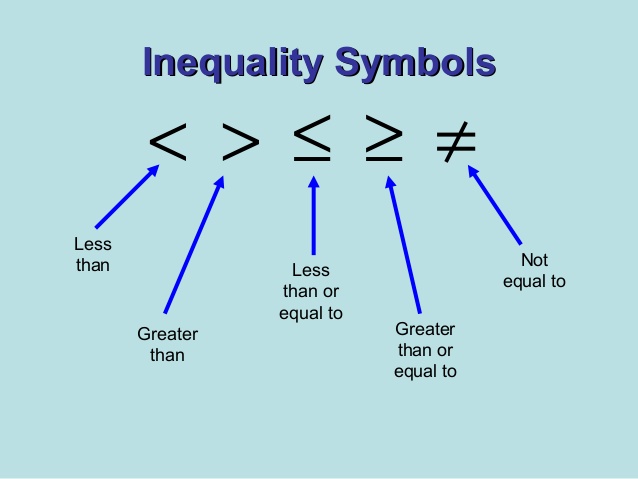
Take a and b to be any number points on number line below:
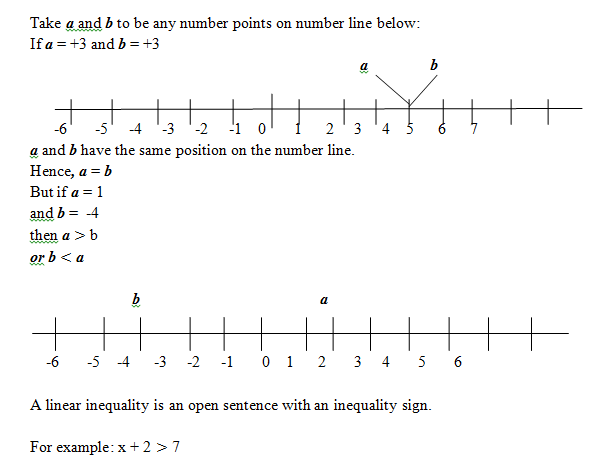
Example:
The radius of a circle is less than 5m. What can be said about?
Its circumference?
Its area?
Solution
r < 5m
Circumference = 2πr
Circumference < 10 πm
Area=πr^2
Area < 25πm2
EVALUATION:
(1) State whether each of the following is true or false.
(a) 12 > 5
(b) 0 > -4 -3
(c) -5 > 7
(d) -2 < -4

(2) Eraser cost 7 kobo each, x kobo is not enough to buy an eraser but a boy with y kobo is able to buy an eraser. Write down 3 different inequalities in terms of a or b or both.
Graphs of Inequalities in one Variable

SOLUTION OF INEQUALITIES
Example1:
Solve the inequality x + 4 < 6
Solution
x + 4 < 6
Subtract 4 from both sides.
X + 4-4 < 6 – 4
X < 2
Example 2:
Solve 19 ≥ 4 – 5x
Solution:
19 ≥ 4 – 5x
Subtract 4 from both sides
19-4 ≥ 4-4 -5x
15 ≥ -5x
Divide both sides by -5 and reverse the inequality sign.
15/(-5)≤ (-5x)/(-5)
-3 ≤ x
If -3 ≤ x, then x ≥ -3.

https://www.youtube.com/watch?v=0S68iRQxuWw
ASSIGNMENT:
NEW GENERAL MATHEMATICS FOR JSS 2 (UBE EDITION)
PG. 209 – 213.
Ex. 22f 1-5; 22g 1-5; 22h 1-5
TOPIC Inequalities
REFERENCE BOOK Macmillan Progressive Mathematics for JS1,Page 69
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to :
(1) Use the inequality symbols ≥ , ≤, ≠, and ≠ correctly.
(2) Write and interpret linear inequality in one variable.
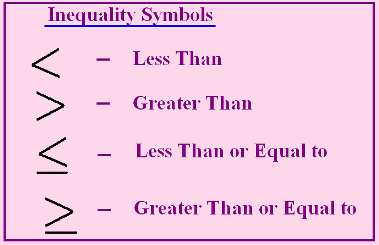
CONTENTS
≤ less than or equal to
≥ greater than or equal to
≠ not equal to
5 + 5 ≠ 7
3 + 6 ≥ 8
40 ≤ 94
Write the appropriate symbols in the boxes.
(a) 3 is less than 7 □
(b) 6 + 8 is greater than 10 □
(c) 41 is not equal to 33 □
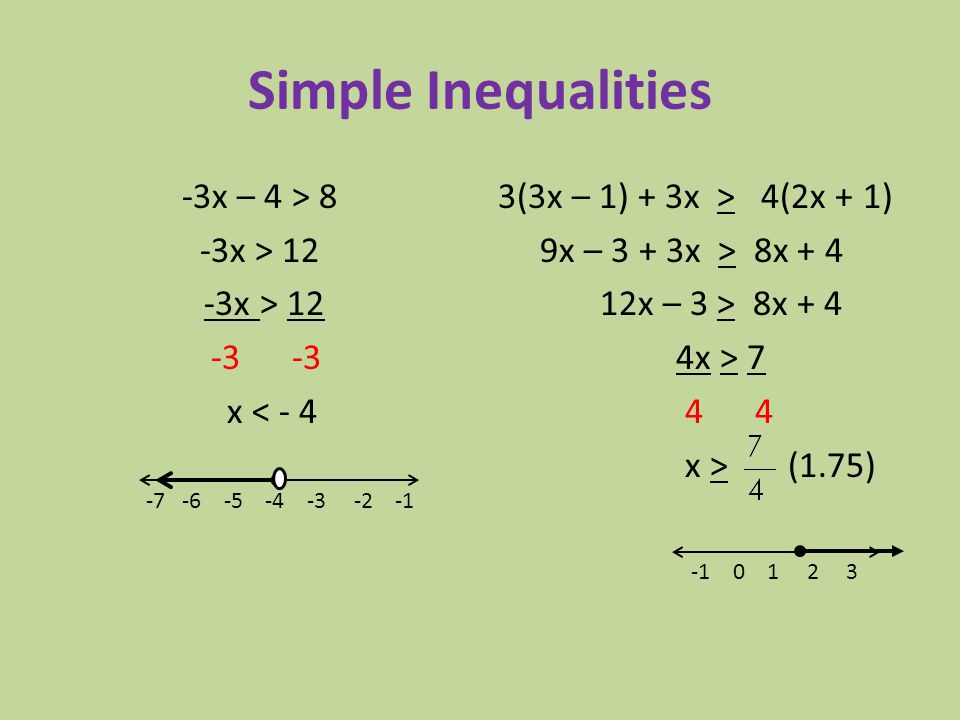
EVALUATION This lesson is evaluated from New General Mathematics for JS2 Page 209, ex. 22a , questions 2a - j.
https://youtu.be/wcBwdz-ZBaM
ASSIGNMENT New General Mathematics for JS2, Page 210, ex. 22a, Questions 7a - i
Study More...
practice test
Quiz 1
Quiz 2
Quiz 3
LESSON 10
TOPIC Graphs of inequalities
REFERENCE BOOK Macmillan Progressive Mathematics forJS2, Page 74
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to show the graphs of linear inequalities in one variable on the number line.

CONTENTS
x ≤ 2
-3 -2 -1 0 +1 +2 +3
(a)
-1 0 +1 +2 +3 +4 x ≥ 0


EVALUATION The lesson is evaluated from New General Mathematics for JS2, Page 212, Ex 22d Questions a - e
ASSIGNMENT New General Mathematics for JS2 PAGE 212, Ex 22d, Questions 2a - e
further studies
Study More...
Study More...
practice test
Practice More...
Practice More...
view slide show
https://docs.google.com/presentation/d/ ... sp=sharing
https://www.youtube.com/watch?v=AjZzACaeIco
LESSON 11
TOPIC Solution of inequalities (Balance method)
REFERENCE BOOK Macmillan Progressive Mathematics for JS2 Page 70.
BEHAVIOURAL OBJECTIVE: At the end of this lesson, students should be able to solve linear inequalities in one variable.

CONTENTS
EXAMPLE: (a). Solve the inequality: x + 4 ≤ 6
Subtract 4 from both sides.
X + 4 - 4 ≤ 6 - 4
X ≤ 2
(b). Solve 6 ≤ 2x - 1 and show your answer on a graph.
6 ≤ 2x - 1
Add 1 to both sides
7≤ 2x
7/2 ≤ x
3.5 ≤ x or x≥ 3.5

https://youtu.be/97-HZQabPvc
EVALUATION The lesson is evaluated from New General Mathematics for JS2 Page 213 Ex 22e questions 1- 5.
ASSIGNMENT New General Mathematics for JS2 Page 213, Ex 22e questions 6 - 9
further studies
Study More...
http://www.youtube.com/watch?v=UeQeHF7gojU
LESSON 12
TOPIC MULTIPLICATION AND DIVISION BY NEGATIVE NUMBERS
REFERENCE BOOK Macmillan Progressive Mathematics for JS2 Page 76.
BEHAVIOURAL OBJECTIVE: At the end of this lesson, students should be able to solve inequalities involving multiplication and division by negative numbers.

CONTENTS
(a) Solve 5 - x ≥ 3
Subtract 5 from both sides
5 - 5 - x ≥ 3 -5
- X ≥ -2
Multiply both sides -1 and reverse the inequality
i e x ≤ 2
Page 215 Ex 22g Questions 1-5
ASSIGNMENT New General Mathematics for JS2, Page 214 Ex 22g, Questions 6-9.

further studies
Study More...
Study More...
practice test
Practice More...
watch video
https://youtu.be/I6Njd2XWF5E
LESSON 13
TOPIC Solving word problems involving inequalities.
REFERENCE BOOK Macmillan Progressive Mathematics for JS2 , Page 69.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to solve word problems on inequalities.

CONTENTS

(a) If 7 is subtracted from a certain number, the result is less than 15. Find the values of the number.
Solution: Let y represent the number.
Y - 7 ≤ 15
Y ≤ 15 + 7
Y ≤ 22

EVALUATION: The lesson is evaluated from New General Mathematics for JS2 Page 215, Ex 22h, Questions 1- 5
http://www.youtube.com/watch?v=iMKv6jOYut0
ASSIGNMENT: New General Mathematics for JS2 Page 215, Questions 6 - 9.
further studies
Study More...
LESSON 14
TOPIC: LINEAR INEQUALITIES
CONTENT:
Inequalities
Graphs of inequalities
Solution of inequalities
INEQUALITIES
In mathematics, we use the equal s sign, = , to show that quantities are the same. How ever, very often, quantities are different, or unequal. The inequalities symbols are as follows:

Take a and b to be any number points on number line below:

Example:
The radius of a circle is less than 5m. What can be said about?
Its circumference?
Its area?
Solution
r < 5m
Circumference = 2πr
Circumference < 10 πm
Area=πr^2
Area < 25πm2
EVALUATION:
(1) State whether each of the following is true or false.
(a) 12 > 5
(b) 0 > -4 -3
(c) -5 > 7
(d) -2 < -4

(2) Eraser cost 7 kobo each, x kobo is not enough to buy an eraser but a boy with y kobo is able to buy an eraser. Write down 3 different inequalities in terms of a or b or both.
Graphs of Inequalities in one Variable

SOLUTION OF INEQUALITIES
Example1:
Solve the inequality x + 4 < 6
Solution
x + 4 < 6
Subtract 4 from both sides.
X + 4-4 < 6 – 4
X < 2
Example 2:
Solve 19 ≥ 4 – 5x
Solution:
19 ≥ 4 – 5x
Subtract 4 from both sides
19-4 ≥ 4-4 -5x
15 ≥ -5x
Divide both sides by -5 and reverse the inequality sign.
15/(-5)≤ (-5x)/(-5)
-3 ≤ x
If -3 ≤ x, then x ≥ -3.

https://www.youtube.com/watch?v=0S68iRQxuWw
ASSIGNMENT:
NEW GENERAL MATHEMATICS FOR JSS 2 (UBE EDITION)
PG. 209 – 213.
Ex. 22f 1-5; 22g 1-5; 22h 1-5
WEEK 4
LESSON 15
TOPIC: GRAPH
Content:
Plotting points on Cartesian plane
Linear equation in two variables
Graph of linear equation in two variables
PLOTTING POINTS ON CARTESIAN PLANE
Graph is a picture of numerical data. A familiar example is the representation of numbers on the number line. The positions of the number on the line are called points.
CARTESIAN PLANE
This is plane surface with axes drawn on it. The Cartesian is derived from a French philosopher and mathematician who work out the possibility of presenting geometry in a numerical form. His full name is Rene Descartes, hence the name Cartesian
Cartesian plane
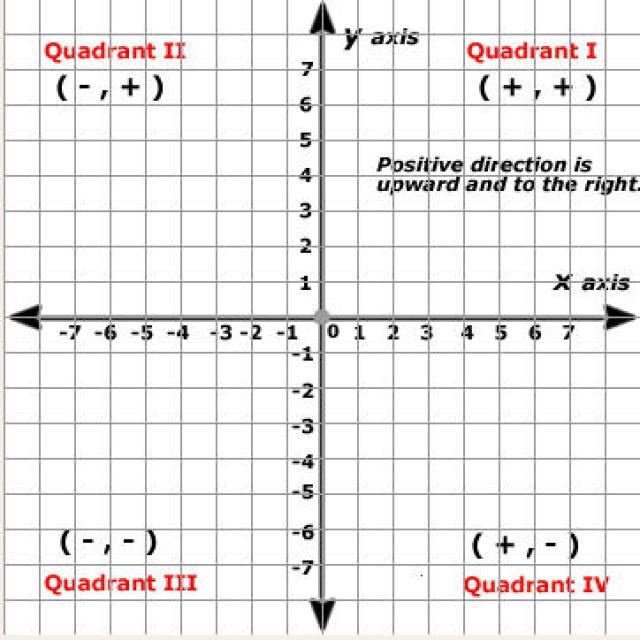
We describe a point on a Cartesian plane by two numbers say (x,y) called coordinates. x is the distance of the point from vertical line called y-axis and y is the distance of the point from horizontal line called x-axis. The figure illustrates more.
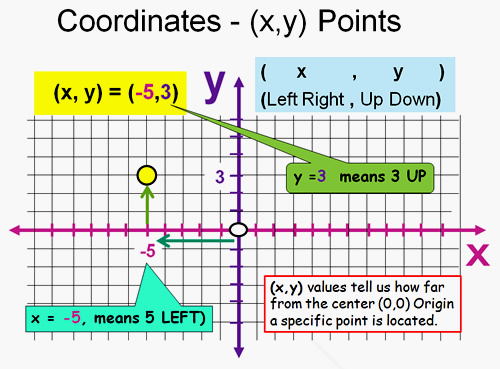
The position of each point is given by an ordered pair of number. These are called co-ordinates of the point. The first number is called the x- coordinate and second number is called y-coordinate. The coordinates are separated by a comma.
A(3,2) B(-2,1) C(-3,-2) D(3,-2)
https://youtu.be/BXhNY0hZmzE
Evaluation:
Plot the following points on a graph:
(2,4), (5,1), (3,4),(1,1)
(6,6), (1,6), (4,4), (1,4)
LINEAR GRAPH
This is also called straight line graph. A linear graph is obtained by plotting the points whose coordinates (x,y) satisfying a linear equation of the form y=ax+c, where a and c are given constants and a≠0.
a= gradient and c=intercept
PLOTTING OF GRAPH
This is the process by which those recorded pairs of points in the in the table of values are now transferred onto the graph paper appropriately.
To do this accurately the following points are considered:
Prepare a table of value for function or equation given
Draw the axes (x-axis and y-axis)
Choose the appropriate scale if not given
Choose any convenient range of your choice for x if not given.
Plot the points according to the calculated coordinate pairs
Join the plotted points using rule for a straight line graph and curve for quadratic graph
Example:
Plot the graph of the function y=x-3 using values of x from -3 to 2
Solution:
x -3 -2 -1 0 1 2
-3 -3 -3 -3 -3 -3 -3
y -6 -5 -4 -3 -2 -1
https://www.youtube.com/watch?v=9Uc62CuQjc4
EVALUATION:
Draw the graphs of the following functions:
y=x+1 b. y=3x-5 c. 2y=4x+4,3y=-3x
ASSIGNMENT:
New General Mathematics JSS-2 UBE Edition page102-104.
New General Mathematics JSS-2 UBE Edition page102, Ex. 12a Q1 to Q4
LESSON 16
TOPIC: Graph of Linear Equations.
REFERENCE BOOK New General Mathematics for JSS 2, Page 217.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to prepare tables of values for linear equations in two variables.
CONTENTS
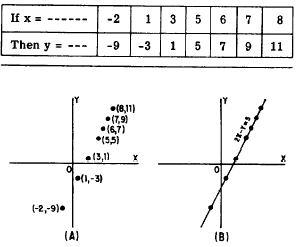
Equations and tables of values.
Y = 2x - 5 is an equation in x and y. Prepare a table of values from x = -2 to +4.
X -2 -1 0 1 2 3 4
2x - 5 -9 -7 -5 -3 -1 1 3
The table contains the following set of ordered pairs of corresponding values of x and y.
(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1), (3, 1) and (4, 3).
EVALUATION: Prepare tables of values for the following equations for x = -3 to +3
(a) Y = x - 5
(b) Y = 2 + 5x
(c) Y = 4 - 2x
(d) Y = x - 2
https://youtu.be/MXV65i9g1Xg
ASSIGNMENT: New General Mathematics for JS2, Page 220, ex 23b, Questions 4, 5 and 6.
practice test
Practice More...
watch videos
https://www.youtube.com/watch?v=YGVUVPOKLws
http://www.youtube.com/watch?v=cNcO64sIjlk
LESSON 17
TOPIC: Plotting points from the tables of value.
REFERENCE BOOK Macmillan Progressive Mathematics for JS2 ,Page 86.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to plot points from tables of values.
CONTENTS
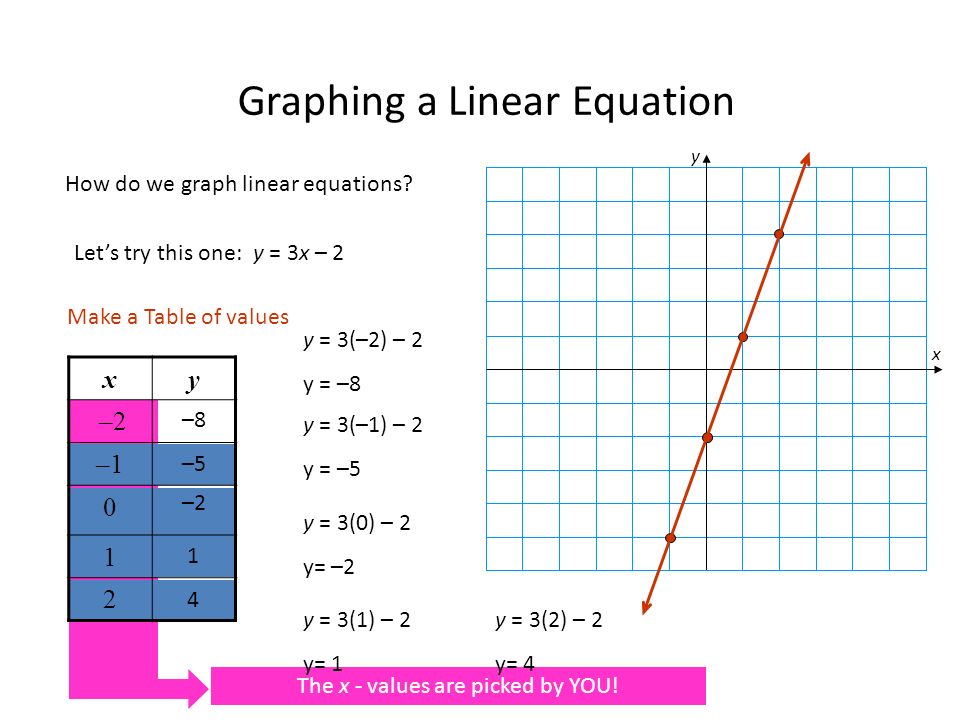
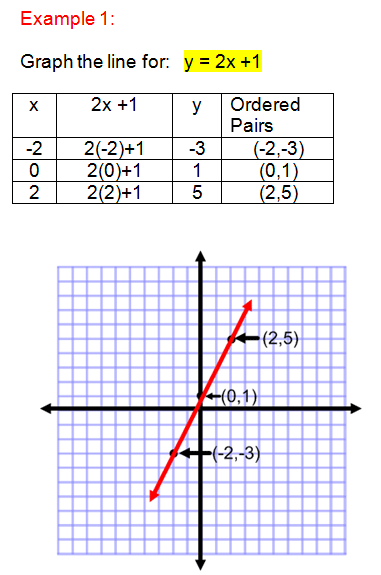
Example: Draw the graph of y = 2x + 1 from -2 to 2
Solution Table of values
X -2 -1 0 1 2
Y -3 -1 1 3 5
Steps:
(a) Draw the x and y axis.
(b) Plot the values of x against that of y.
(c) Join the points with a ruler.
https://youtu.be/Ru5fWYVvoBk
EVALUATION
(a) Draw the graph of y = 3x + 2 from -3 to 3
(b) Draw the graph of y = 1 + 2x from -2 to 2
ASSIGNMENT Draw the graph of y = x - 5 from -3 to 2
Draw the graph of the equation 5x + 2y - 6 =0 for x = -2, 0, +2.
further studies
http://www.slideshare.net/bigpassy/plot ... om-ttables
Study More...
Study More...
practice test
Practice More...
watch video
http://www.youtube.com/watch?v=Ru5fWYVvoBk
LESSON 18
TOPIC: Intersection with the axes.
REFERENCE BOOK: New General Mathematics for JS2, Page 221.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to find the x and y intercepts of given lines.
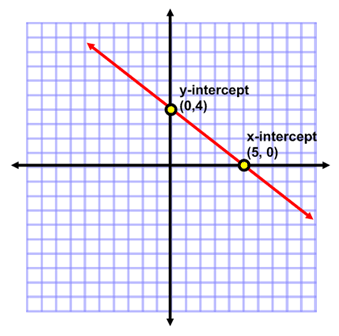
CONTENTS
Find the x and y intercepts of the line y = 4x - 9
The x-intercept is where y = 0.
When y = 0, 0 = 4x - 9
4x = 9
X = 2.25 (the x-intercept)
The y intercept is the constant term y = 4x -9 i.e, -9.
http://www.youtube.com/watch?v=mxBoni8N70Y
EVALUATION
(a) What are the x and y intercepts of the line y = 2x - 5 ?
(b) Find the x and y intercepts of the lines y = 20 - 10x and
(c) Y = -10 -10x
ASSIGNMENT Answer the following questions from New General Mathematics for JS2 Page 221, Ex 23c Numbers 1 a - d.
further studies
Study More...
practice test
Practice More...
Practice More...
LESSON 19
TOPIC Plotting points from the tables of values.
REFERENCE BOOK: New General Mathematics for JS2 Page 221.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to plot points from tables of values.
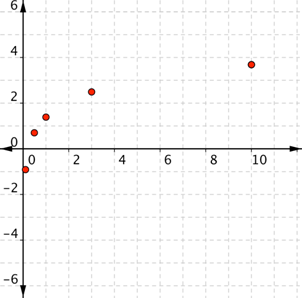
CONTENTS
Draw the graph of y = 9 - 2x from -2 to +3
TABLE OF VALUES
X -2 -1 0 1 2 3
9 - 2X 13 11 9 7 5 3
Ordered pairs of x and y are: (-2, 13), (-1, 11), (0, 9),
(1, 7), (2, 5), (3, 3)
EVALUATION: Draw the graphs of the following equations for values of x from -3 to +3.
(a) Y = x + 5
(b) Y = 5 - 3x
https://youtu.be/-u55GD_sGLA
ASSIGNMENT: Draw the graphs of the following equations for values of x from -3 to +3.
(a) Y = 5 + 2x
(b) Y = 2x - 3
further studies
Study More...
LESSON 20
TOPIC: Graph of Linear Equation(Revision)
REFERENCE BOOK: Macmillan Progressive Mathematics for JS2.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to plot graphs of given linear equations.
CONTENTS
Example: Plot the graph of y = 4x - 5 from -2 to +4 and use the graph to find the coordinates of the points where the line cuts the axes.
(2) Draw the graphs of y = 4x and y =x + 5 on the same axes.
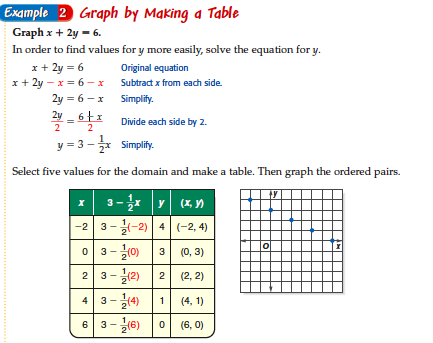
EVALUATION: New General Mathematics for JS2 Page 219, Ex. 23a, Questions 3a - c.
ASSIGNMENT: New General Mathematics for JS2 Page 219, Ex 23B, QUESTIONS 1 - 3.
further studies
Study More...
Study More...
plot graph for any equation automatically
Equation Grapher...
LESSON 21
TOPIC: GRAPHS
CONTENT:
linear graphs from real life situation
Quantitative reasoning on linear graph
LINEAR GRAPHS FROM REAL LIFE SITUATION
Example
A student walks along a road at a speed of 120m per minute.
a. Make a table of values showing how far the students have walked after 0, 1, 2, 3, 4, 5 minutes.
b. Using a scale of 1cm to 1min on the horizontal axis and 1cm to 100cm on the vertical axis, draw a graph of this information.
c. Use the graph to find the following:
i. How far the student has walked after 2.6min
ii. How long it takes the student to walk 500m.
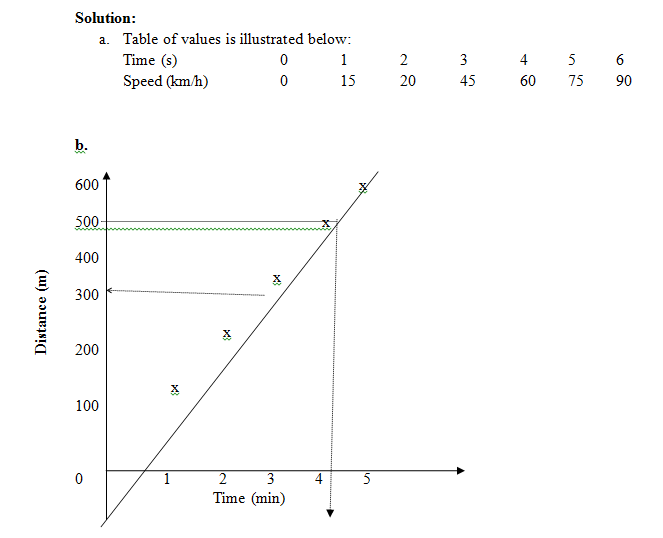
(c) i. 2.6 min corresponds to 310m (approximately). The student has walked about 310m after 2.6min.
ii. 500m corresponding to 4.2min (approximate). The student takes about 4.2min to walk 500m.
EVALUATION:
A girl walks along a road at a speed of 100m per minute.
a. Copy and complete the table below:
Time (min) 0 1 2 3 4 5 6
Distance (m) 0 100 200
b. Using a scale of 2cm to 1min on the horizontal axis and 2cm to 100m on the vertical axis, draw a graph of the information.
c. Use your graph to find i. how far the girl has walked after 5.7 min, ii. how long it takes her to walk 335m
https://youtu.be/S5iz0yNtrzk
ASSIGNMENT:
New General Mathematics JSS 2 (UBE Edition), pg 119- 136
Ex. 14a. Q5; 14b.Q 2; 14c. Q1 page 121-125
TOPIC: GRAPH
Content:
Plotting points on Cartesian plane
Linear equation in two variables
Graph of linear equation in two variables
PLOTTING POINTS ON CARTESIAN PLANE
Graph is a picture of numerical data. A familiar example is the representation of numbers on the number line. The positions of the number on the line are called points.
CARTESIAN PLANE
This is plane surface with axes drawn on it. The Cartesian is derived from a French philosopher and mathematician who work out the possibility of presenting geometry in a numerical form. His full name is Rene Descartes, hence the name Cartesian
Cartesian plane

We describe a point on a Cartesian plane by two numbers say (x,y) called coordinates. x is the distance of the point from vertical line called y-axis and y is the distance of the point from horizontal line called x-axis. The figure illustrates more.

The position of each point is given by an ordered pair of number. These are called co-ordinates of the point. The first number is called the x- coordinate and second number is called y-coordinate. The coordinates are separated by a comma.
A(3,2) B(-2,1) C(-3,-2) D(3,-2)
https://youtu.be/BXhNY0hZmzE
Evaluation:
Plot the following points on a graph:
(2,4), (5,1), (3,4),(1,1)
(6,6), (1,6), (4,4), (1,4)
LINEAR GRAPH
This is also called straight line graph. A linear graph is obtained by plotting the points whose coordinates (x,y) satisfying a linear equation of the form y=ax+c, where a and c are given constants and a≠0.
a= gradient and c=intercept
PLOTTING OF GRAPH
This is the process by which those recorded pairs of points in the in the table of values are now transferred onto the graph paper appropriately.
To do this accurately the following points are considered:
Prepare a table of value for function or equation given
Draw the axes (x-axis and y-axis)
Choose the appropriate scale if not given
Choose any convenient range of your choice for x if not given.
Plot the points according to the calculated coordinate pairs
Join the plotted points using rule for a straight line graph and curve for quadratic graph
Example:
Plot the graph of the function y=x-3 using values of x from -3 to 2
Solution:
x -3 -2 -1 0 1 2
-3 -3 -3 -3 -3 -3 -3
y -6 -5 -4 -3 -2 -1
https://www.youtube.com/watch?v=9Uc62CuQjc4
EVALUATION:
Draw the graphs of the following functions:
y=x+1 b. y=3x-5 c. 2y=4x+4,3y=-3x
ASSIGNMENT:
New General Mathematics JSS-2 UBE Edition page102-104.
New General Mathematics JSS-2 UBE Edition page102, Ex. 12a Q1 to Q4
LESSON 16
TOPIC: Graph of Linear Equations.
REFERENCE BOOK New General Mathematics for JSS 2, Page 217.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to prepare tables of values for linear equations in two variables.

CONTENTS
Equations and tables of values.
Y = 2x - 5 is an equation in x and y. Prepare a table of values from x = -2 to +4.
X -2 -1 0 1 2 3 4
2x - 5 -9 -7 -5 -3 -1 1 3
The table contains the following set of ordered pairs of corresponding values of x and y.
(-2, -9), (-1, -7), (0, -5), (1, -3), (2, -1), (3, 1) and (4, 3).

EVALUATION: Prepare tables of values for the following equations for x = -3 to +3
(a) Y = x - 5
(b) Y = 2 + 5x
(c) Y = 4 - 2x
(d) Y = x - 2
https://youtu.be/MXV65i9g1Xg
ASSIGNMENT: New General Mathematics for JS2, Page 220, ex 23b, Questions 4, 5 and 6.
practice test
Practice More...
watch videos
https://www.youtube.com/watch?v=YGVUVPOKLws
http://www.youtube.com/watch?v=cNcO64sIjlk
LESSON 17
TOPIC: Plotting points from the tables of value.
REFERENCE BOOK Macmillan Progressive Mathematics for JS2 ,Page 86.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to plot points from tables of values.

CONTENTS
Example: Draw the graph of y = 2x + 1 from -2 to 2
Solution Table of values
X -2 -1 0 1 2
Y -3 -1 1 3 5
Steps:
(a) Draw the x and y axis.
(b) Plot the values of x against that of y.
(c) Join the points with a ruler.
https://youtu.be/Ru5fWYVvoBk
EVALUATION
(a) Draw the graph of y = 3x + 2 from -3 to 3
(b) Draw the graph of y = 1 + 2x from -2 to 2
ASSIGNMENT Draw the graph of y = x - 5 from -3 to 2
Draw the graph of the equation 5x + 2y - 6 =0 for x = -2, 0, +2.
further studies
http://www.slideshare.net/bigpassy/plot ... om-ttables
Study More...
Study More...
practice test
Practice More...
watch video
http://www.youtube.com/watch?v=Ru5fWYVvoBk
LESSON 18
TOPIC: Intersection with the axes.
REFERENCE BOOK: New General Mathematics for JS2, Page 221.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to find the x and y intercepts of given lines.

CONTENTS
Find the x and y intercepts of the line y = 4x - 9
The x-intercept is where y = 0.
When y = 0, 0 = 4x - 9
4x = 9
X = 2.25 (the x-intercept)
The y intercept is the constant term y = 4x -9 i.e, -9.
http://www.youtube.com/watch?v=mxBoni8N70Y
EVALUATION
(a) What are the x and y intercepts of the line y = 2x - 5 ?
(b) Find the x and y intercepts of the lines y = 20 - 10x and
(c) Y = -10 -10x
ASSIGNMENT Answer the following questions from New General Mathematics for JS2 Page 221, Ex 23c Numbers 1 a - d.
further studies
Study More...
practice test
Practice More...
Practice More...
LESSON 19
TOPIC Plotting points from the tables of values.
REFERENCE BOOK: New General Mathematics for JS2 Page 221.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to plot points from tables of values.

CONTENTS
Draw the graph of y = 9 - 2x from -2 to +3
TABLE OF VALUES
X -2 -1 0 1 2 3
9 - 2X 13 11 9 7 5 3
Ordered pairs of x and y are: (-2, 13), (-1, 11), (0, 9),
(1, 7), (2, 5), (3, 3)

EVALUATION: Draw the graphs of the following equations for values of x from -3 to +3.
(a) Y = x + 5
(b) Y = 5 - 3x
https://youtu.be/-u55GD_sGLA
ASSIGNMENT: Draw the graphs of the following equations for values of x from -3 to +3.
(a) Y = 5 + 2x
(b) Y = 2x - 3
further studies
Study More...
LESSON 20
TOPIC: Graph of Linear Equation(Revision)
REFERENCE BOOK: Macmillan Progressive Mathematics for JS2.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to plot graphs of given linear equations.
CONTENTS
Example: Plot the graph of y = 4x - 5 from -2 to +4 and use the graph to find the coordinates of the points where the line cuts the axes.
(2) Draw the graphs of y = 4x and y =x + 5 on the same axes.


EVALUATION: New General Mathematics for JS2 Page 219, Ex. 23a, Questions 3a - c.
ASSIGNMENT: New General Mathematics for JS2 Page 219, Ex 23B, QUESTIONS 1 - 3.
further studies
Study More...
Study More...
plot graph for any equation automatically
Equation Grapher...
LESSON 21
TOPIC: GRAPHS
CONTENT:
linear graphs from real life situation
Quantitative reasoning on linear graph
LINEAR GRAPHS FROM REAL LIFE SITUATION
Example
A student walks along a road at a speed of 120m per minute.
a. Make a table of values showing how far the students have walked after 0, 1, 2, 3, 4, 5 minutes.
b. Using a scale of 1cm to 1min on the horizontal axis and 1cm to 100cm on the vertical axis, draw a graph of this information.
c. Use the graph to find the following:
i. How far the student has walked after 2.6min
ii. How long it takes the student to walk 500m.

(c) i. 2.6 min corresponds to 310m (approximately). The student has walked about 310m after 2.6min.
ii. 500m corresponding to 4.2min (approximate). The student takes about 4.2min to walk 500m.
EVALUATION:
A girl walks along a road at a speed of 100m per minute.
a. Copy and complete the table below:
Time (min) 0 1 2 3 4 5 6
Distance (m) 0 100 200
b. Using a scale of 2cm to 1min on the horizontal axis and 2cm to 100m on the vertical axis, draw a graph of the information.
c. Use your graph to find i. how far the girl has walked after 5.7 min, ii. how long it takes her to walk 335m
https://youtu.be/S5iz0yNtrzk
ASSIGNMENT:
New General Mathematics JSS 2 (UBE Edition), pg 119- 136
Ex. 14a. Q5; 14b.Q 2; 14c. Q1 page 121-125
WEEK 5
LESSON 22
TOPIC: PLANE SHAPES ON CARTESIAN PLANE
Content:
Plotting and joining of points to form plane shapes
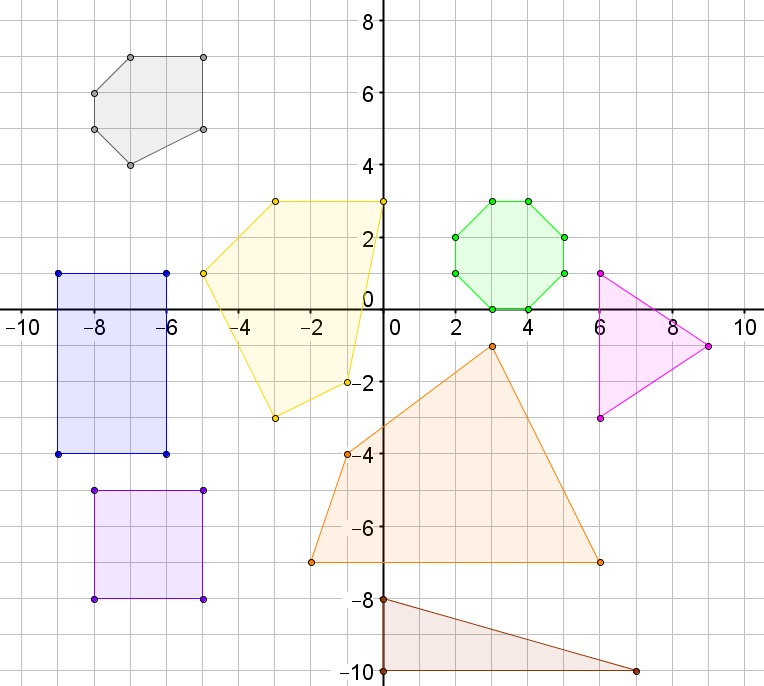
PLOTTING AND JOINING OF POINTS TO FORM PLANE SHAPES
Examples:
a. Plot the points: P (-5, 3) Q (3, 5) R (-4,-4)
b. Join the plotted points
c. Name the shape obtained
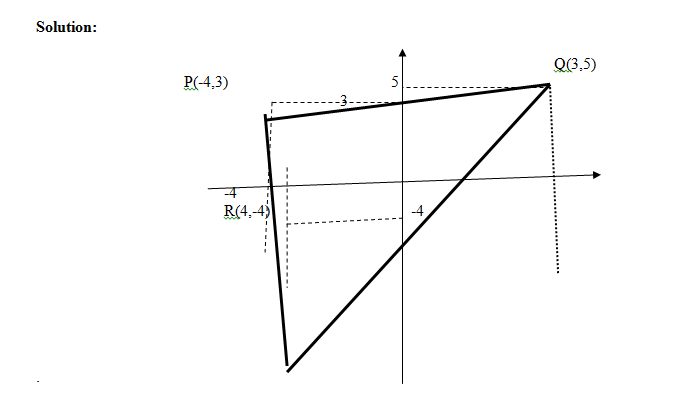
EVALUATION:
Using a graph paper, draw axes OX and OY and label the x-axis -7 to 7 and y-axis from -5 to 5. Using the same scale for each axis, plot the following points and join them together in the given order.
1. A(2,5) B(-5,-2) C(4,4)
2. P(-5,2) Q(0,5) R(7,2) S(0,0)
3. Name each in questions (1) and (2) above
https://youtu.be/k5etrWdIY6o
https://youtu.be/8V-PdgS2GKc
READING ASSIGNMENT:
New General Mathematics JSS-2 UBE Edition page104-109
WORKING ASSIGNMENT:
New General Mathematics JSS-2 UBE Edition page108, Ex. 12d Q1 to Q6
LESSON 23
TOPIC: PLANE FIGURES/SHAPES
CONTENT:
Properties of Quadrilateral (i.e. parallelogram, rhombus, and kite)
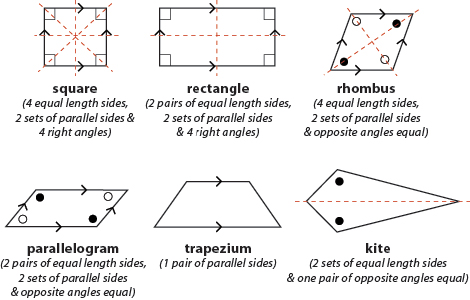
QUADRILATERAL
Any four sided plane figure is called a quadrilateral.
Examples of quadrilaterals are:
a. PARALLELOGRAM
A parallelogram is a quadrilateral whose pairs are equal and parallel.
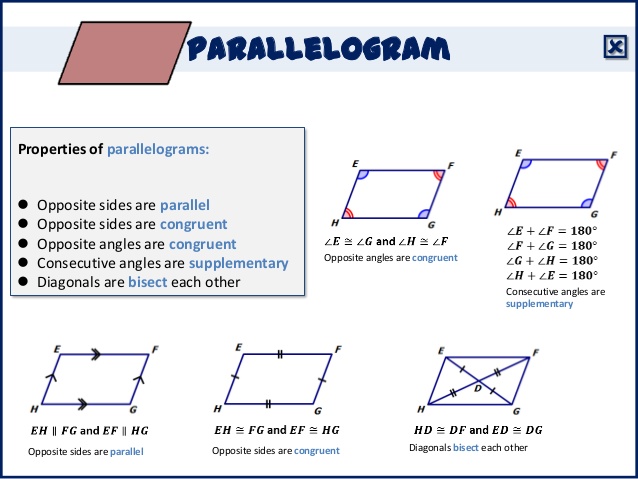
PROPERTIES OF PARALLELOGRAM
i. Its opposite sides are parallel and equal
ii. Its opposite angles are equal
iii. Its diagonals bisect each other
iv. Each diagonal bisects the parallelogram into two congruent triangles
v. The (4) angles together add up to 3600
https://youtu.be/yiREqzDsMP8
Consider the parallelogram below:
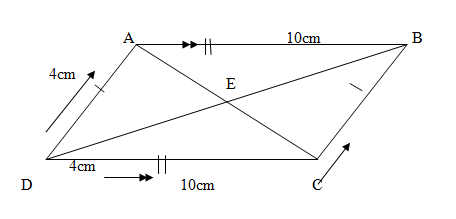
Line AB =Line DC = 10cm
Line AB is parallel to line DC
Line AD = Line BC = 4cm
Line AD is parallel to line BC
Angle BAD = Angle BCD
Angle ADC = Angle ABC
Diagonal AC divides the parallelogram ABCD into two congruent triangles ABC and ADC
Diagonal DB divides the parallelogram ABCD into two congruent triangles DAB and DCB
The diagonals bisect each other at point E i.e.
AE = EC = and DE = EB
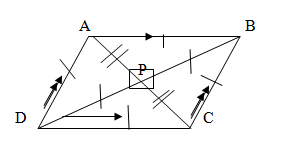
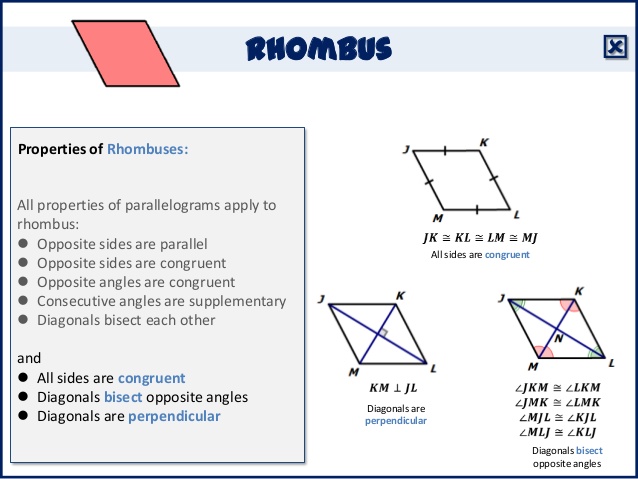
b. RHOMBUS
A rhombus is a quadrilateral which has four sides equal length.
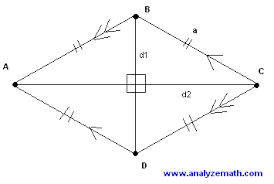
PROPERTIES OF RHOMBUS
1. All four sides are equal in length.
2. The opposite angles are equal.
3. The diagonals are the lines of symmetry.
4. The diagonals bisect each other at right angles.
https://youtu.be/rzfIxKAMWUo
Line AB = line BC = line DC = line AD, i.e.
AB = BC= DC = AD
AD is parallel to BC
AB is parallel to DC
<DAB = <BCD, and <DPC = <APD
<APB = <BPC = <DPC = <APD = 900
PA = PC and PB = PD
c. KITE
A kite is a quadrilateral in which one diagonal is a line of symmetry.
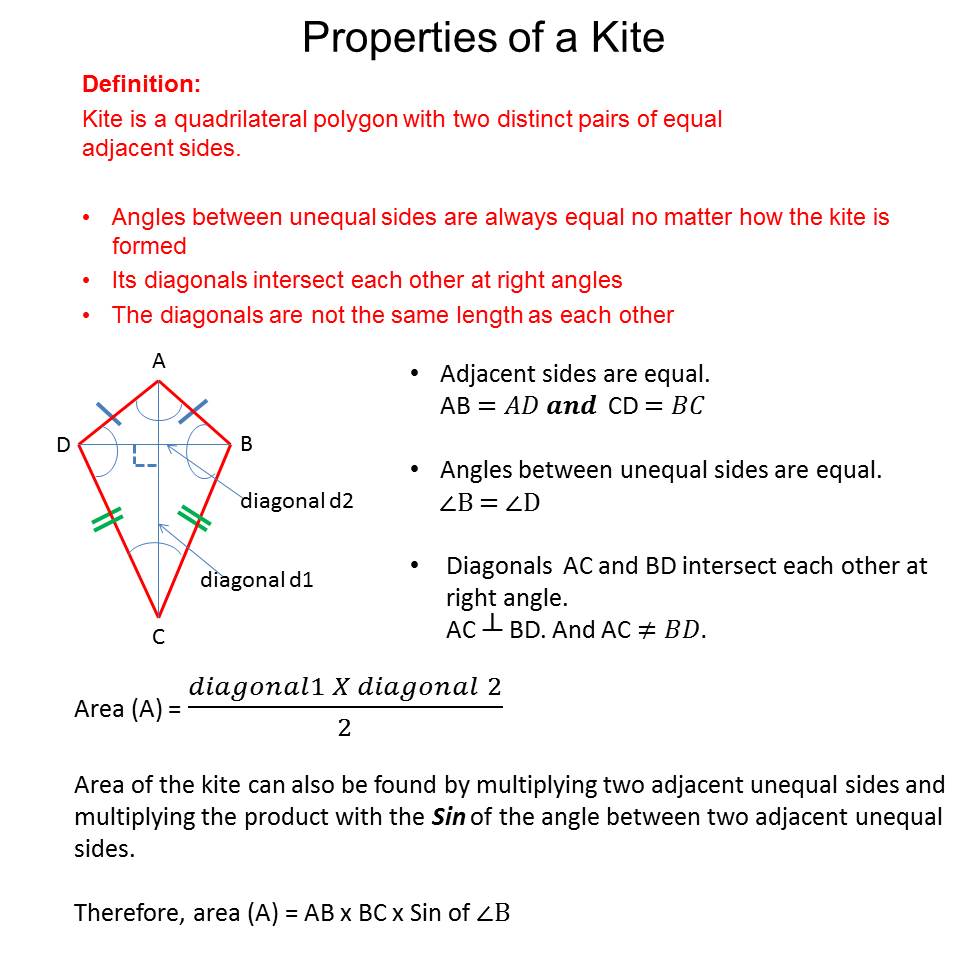
https://youtu.be/HPuI46Frvgg
EVALUATION / ACTIVITIES:
Draw a parallelogram on a cardboard paper such that its diagonals meet C. then cut out the parallelogram along the diagonals. What do you notice?
ASSIGNMENT:
New General Mathematics for JSS 2 (UBE Edition) , pg 32-38
New General Mathematics for JSS 2 (UBE Edition) , pg 37
Ex. 3d Q1-Q10
TOPIC: PLANE SHAPES ON CARTESIAN PLANE
Content:
Plotting and joining of points to form plane shapes

PLOTTING AND JOINING OF POINTS TO FORM PLANE SHAPES
Examples:
a. Plot the points: P (-5, 3) Q (3, 5) R (-4,-4)
b. Join the plotted points
c. Name the shape obtained

EVALUATION:
Using a graph paper, draw axes OX and OY and label the x-axis -7 to 7 and y-axis from -5 to 5. Using the same scale for each axis, plot the following points and join them together in the given order.
1. A(2,5) B(-5,-2) C(4,4)
2. P(-5,2) Q(0,5) R(7,2) S(0,0)
3. Name each in questions (1) and (2) above
https://youtu.be/k5etrWdIY6o
https://youtu.be/8V-PdgS2GKc
READING ASSIGNMENT:
New General Mathematics JSS-2 UBE Edition page104-109
WORKING ASSIGNMENT:
New General Mathematics JSS-2 UBE Edition page108, Ex. 12d Q1 to Q6
LESSON 23
TOPIC: PLANE FIGURES/SHAPES
CONTENT:
Properties of Quadrilateral (i.e. parallelogram, rhombus, and kite)

QUADRILATERAL
Any four sided plane figure is called a quadrilateral.
Examples of quadrilaterals are:
a. PARALLELOGRAM
A parallelogram is a quadrilateral whose pairs are equal and parallel.

PROPERTIES OF PARALLELOGRAM
i. Its opposite sides are parallel and equal
ii. Its opposite angles are equal
iii. Its diagonals bisect each other
iv. Each diagonal bisects the parallelogram into two congruent triangles
v. The (4) angles together add up to 3600
https://youtu.be/yiREqzDsMP8
Consider the parallelogram below:

Line AB =Line DC = 10cm
Line AB is parallel to line DC
Line AD = Line BC = 4cm
Line AD is parallel to line BC
Angle BAD = Angle BCD
Angle ADC = Angle ABC
Diagonal AC divides the parallelogram ABCD into two congruent triangles ABC and ADC
Diagonal DB divides the parallelogram ABCD into two congruent triangles DAB and DCB
The diagonals bisect each other at point E i.e.
AE = EC = and DE = EB
b. RHOMBUS
A rhombus is a quadrilateral which has four sides equal length.

PROPERTIES OF RHOMBUS
1. All four sides are equal in length.
2. The opposite angles are equal.
3. The diagonals are the lines of symmetry.
4. The diagonals bisect each other at right angles.

https://youtu.be/rzfIxKAMWUo
Line AB = line BC = line DC = line AD, i.e.
AB = BC= DC = AD
AD is parallel to BC
AB is parallel to DC
<DAB = <BCD, and <DPC = <APD
<APB = <BPC = <DPC = <APD = 900
PA = PC and PB = PD

c. KITE
A kite is a quadrilateral in which one diagonal is a line of symmetry.

https://youtu.be/HPuI46Frvgg
EVALUATION / ACTIVITIES:
Draw a parallelogram on a cardboard paper such that its diagonals meet C. then cut out the parallelogram along the diagonals. What do you notice?
ASSIGNMENT:
New General Mathematics for JSS 2 (UBE Edition) , pg 32-38
New General Mathematics for JSS 2 (UBE Edition) , pg 37
Ex. 3d Q1-Q10
WEEK 6
LESSON 24
MAIN TOPIC: Cylinders and cones
SPECIFIC TOPIC: Surface area of cylinder
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the curved surface area of cylinders
REFERENCE BOOK: New General Maths for JSS2, page 184
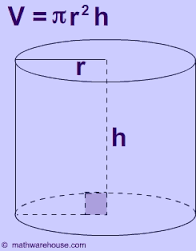
CONTENT (View Content below)

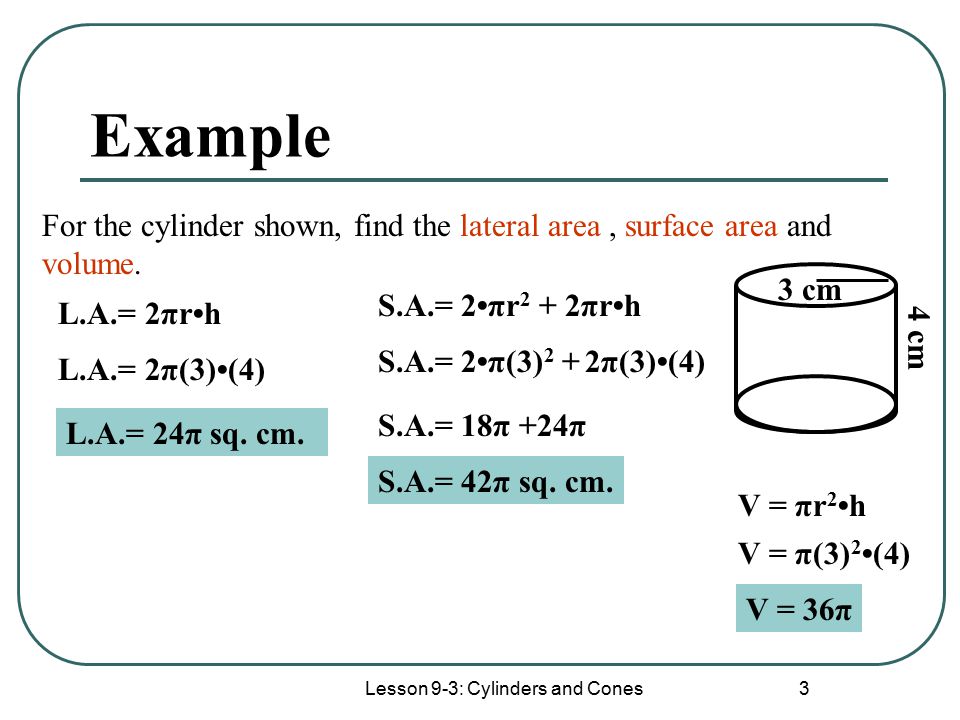
ASSIGNMENT: New General Maths for JSS2, page 185. Ex 19b. Nos 1, b,c and number 2
further studies
Study More...
Study More...
Study More...
watch video
http://www.youtube.com/watch?v=gi7aaZ87EoQ
LESSON 25
TOPIC: Total surface area of cylinders base
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the total surface area of cylinders base.

CONTENT (View Below)


ASSIGNMENT: New General Maths for JSS 2, page 185, numbers 6a, b & c
https://youtu.be/6DXfPk8Kzww
further studies
Study More...
practice test
Practice More...
Practice More...
LESSON 26
TOPIC: Volume of a Cylinder
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to calculate the volume of cylinders

CONTENT (View below)


https://youtu.be/qJwecTgce6c
EVALUATION
a. Calculate the volume of a cylinder which is 8cm long and 3.5cm in diameter
b. The tank on a petrol lorry is cylinder 2m in diameter and 7m long
a. Calculate its volume in m3
b. Find its capacity in kilolitres
ASSIGNMENT: New General Maths for JSS2, page 187 Q 3 & 5
further studies
Study More...
Study More...
practice test
Practice More...
watch video
http://www.youtube.com/watch?v=O5e9RkiXJwI
LESSON 27
TOPIC: Harder problems on volume of cylinders
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to solve harder problems on volume of cylinders
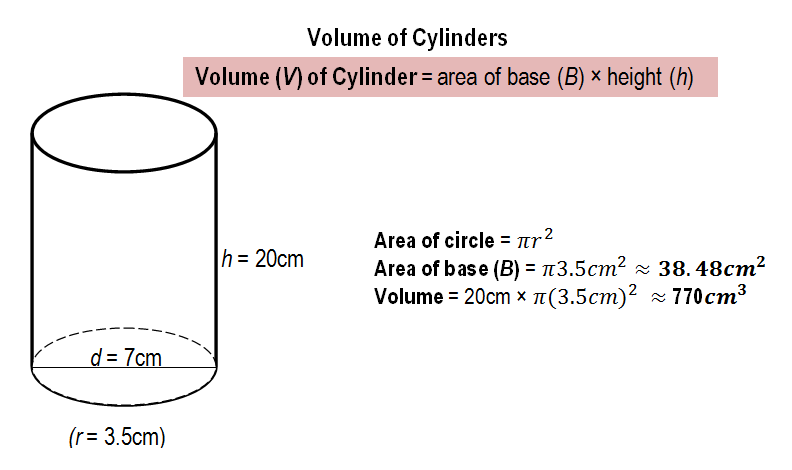
CONTENT (View below)


EVALUATION
a. 99litres of oil are poured into a cylindrical drum 60cm in diameter. How deep is the oil in the drum?
b. A cylindrical pipe is 1m long and 8cm in diameter. Find:
a. Its volume in cm3
b. Its mass in grammes, if 1cm3 of the wood has a mass of 0.7g
https://youtu.be/y3TjAHV7esk
ASSIGNMENT: New General Maths for JSS2, page 187, Q8 & 9
further studies
Study More...
Study More...
MAIN TOPIC: Cylinders and cones
SPECIFIC TOPIC: Surface area of cylinder
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the curved surface area of cylinders
REFERENCE BOOK: New General Maths for JSS2, page 184

CONTENT (View Content below)


ASSIGNMENT: New General Maths for JSS2, page 185. Ex 19b. Nos 1, b,c and number 2
further studies
Study More...
Study More...
Study More...
watch video
http://www.youtube.com/watch?v=gi7aaZ87EoQ
LESSON 25
TOPIC: Total surface area of cylinders base
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to calculate the total surface area of cylinders base.

CONTENT (View Below)


ASSIGNMENT: New General Maths for JSS 2, page 185, numbers 6a, b & c
https://youtu.be/6DXfPk8Kzww
further studies
Study More...
practice test
Practice More...
Practice More...
LESSON 26
TOPIC: Volume of a Cylinder
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to calculate the volume of cylinders

CONTENT (View below)


https://youtu.be/qJwecTgce6c
EVALUATION
a. Calculate the volume of a cylinder which is 8cm long and 3.5cm in diameter
b. The tank on a petrol lorry is cylinder 2m in diameter and 7m long
a. Calculate its volume in m3
b. Find its capacity in kilolitres
ASSIGNMENT: New General Maths for JSS2, page 187 Q 3 & 5
further studies
Study More...
Study More...
practice test
Practice More...
watch video
http://www.youtube.com/watch?v=O5e9RkiXJwI
LESSON 27
TOPIC: Harder problems on volume of cylinders
PERFORMANCE OBJECTIVE: At the end of the lesson, students should be able to solve harder problems on volume of cylinders

CONTENT (View below)


EVALUATION
a. 99litres of oil are poured into a cylindrical drum 60cm in diameter. How deep is the oil in the drum?
b. A cylindrical pipe is 1m long and 8cm in diameter. Find:
a. Its volume in cm3
b. Its mass in grammes, if 1cm3 of the wood has a mass of 0.7g
https://youtu.be/y3TjAHV7esk
ASSIGNMENT: New General Maths for JSS2, page 187, Q8 & 9
further studies
Study More...
Study More...
WEEK 7
LESSON 28
TOPIC: SCALE DRAWING
Content:
Scale
Scale drawing
Reading scale drawing Scale
SCALE
A scale simply means the dimension or proportion of objects in comparison to its original or actual size after the drawing. It is widely use in sciences especially in Geography, Biology, Mathematics, Physics, etc.
The scale of a drawing is determined by comparing the length of the drawing with the actual length of the object.
Scale = (Length of the object after drawing)/(corresponding length of object before drawing )
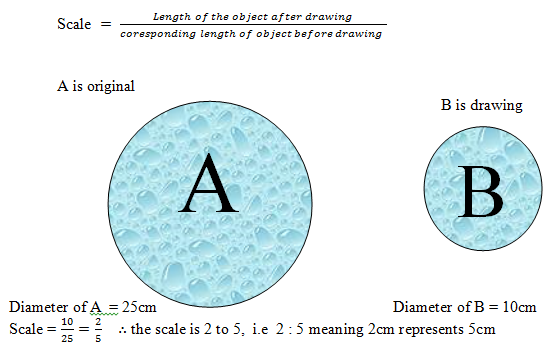
EVALUATION:
Use measurement to find the scale of the following shapes/figures:
SCALE DRAWING
In scale drawing the materials needed are pencil, ruler and set square. The drawings should be on plane sheets or white papers. The dimensions of the actual object should be written on the drawing and a title has to accompany it. However, a rough sketch must be drawn first.
Example:
A measurement of 8000m is drawn to a scale where 1cm represents 500m. Find its length on the drawing.
Solution:
500m is represented by 1cm.
1m is represented by 1/500 cm
8000m is represented by 8000×1/500 cm=16cm
Length on drawing = 16cm.
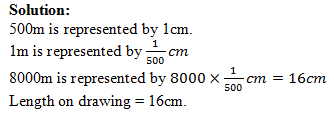
https://youtu.be/vfW_0fdPzps
LESSON 29
READING SCALE DRAWING
Reading scale drawing is common to map reading and interpretation. For instance, scales on maps are often given in the ratio form as 1 : n.
A map of scale 1 : 50 000 means 1cm represents 50 000cm.
This means 1cm on map represents 50 000cm on land.
Map scale =(actual distance)/(distance on map)
Rearranging the above formula we have:
Actual distance = map scale x distance on map
OR Distance on map =(actual distance)/(map scale)

Example:
Change the scale 1 : 800 000 to the form 1cm represents ….km.
Solution:
1:800 000 means 1cm represents 800 000cm.
But 1km = 100 000cm
∴ 1cm represents 800 000 ÷100 000 = 8km
The scale is 1cm represents 8km.
https://youtu.be/65NNqghwrtU
EVALUATION
Two cities are 70km apart. The distance between them is 20cm on the map. What is the scale of the map?
Rewrite the following scales in the form 1:n
1cm represent 20 000cm
1cm represents 500 000cm
ASSIGNMENT:
New General Mathematics JSS 2, UBE Edition, pg 149 – 157
New General Mathematics JSS 2, UBE Edition, pg 153
Ex. 1-3
TOPIC: SCALE DRAWING
Content:
Scale
Scale drawing
Reading scale drawing Scale
SCALE
A scale simply means the dimension or proportion of objects in comparison to its original or actual size after the drawing. It is widely use in sciences especially in Geography, Biology, Mathematics, Physics, etc.
The scale of a drawing is determined by comparing the length of the drawing with the actual length of the object.
Scale = (Length of the object after drawing)/(corresponding length of object before drawing )

EVALUATION:
Use measurement to find the scale of the following shapes/figures:

SCALE DRAWING
In scale drawing the materials needed are pencil, ruler and set square. The drawings should be on plane sheets or white papers. The dimensions of the actual object should be written on the drawing and a title has to accompany it. However, a rough sketch must be drawn first.
Example:
A measurement of 8000m is drawn to a scale where 1cm represents 500m. Find its length on the drawing.
Solution:
500m is represented by 1cm.
1m is represented by 1/500 cm
8000m is represented by 8000×1/500 cm=16cm
Length on drawing = 16cm.
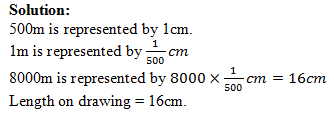
https://youtu.be/vfW_0fdPzps
LESSON 29
READING SCALE DRAWING
Reading scale drawing is common to map reading and interpretation. For instance, scales on maps are often given in the ratio form as 1 : n.
A map of scale 1 : 50 000 means 1cm represents 50 000cm.
This means 1cm on map represents 50 000cm on land.
Map scale =(actual distance)/(distance on map)
Rearranging the above formula we have:
Actual distance = map scale x distance on map
OR Distance on map =(actual distance)/(map scale)

Example:
Change the scale 1 : 800 000 to the form 1cm represents ….km.
Solution:
1:800 000 means 1cm represents 800 000cm.
But 1km = 100 000cm
∴ 1cm represents 800 000 ÷100 000 = 8km
The scale is 1cm represents 8km.

https://youtu.be/65NNqghwrtU
EVALUATION
Two cities are 70km apart. The distance between them is 20cm on the map. What is the scale of the map?
Rewrite the following scales in the form 1:n
1cm represent 20 000cm
1cm represents 500 000cm
ASSIGNMENT:
New General Mathematics JSS 2, UBE Edition, pg 149 – 157
New General Mathematics JSS 2, UBE Edition, pg 153
Ex. 1-3
WEEK 8
LESSON 30
TOPIC STANDARD FORM (Laws of indices).
REFERENCE BOOK New General Mathematics for JS2, Page 23.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to, students should be able to simplify numbers and expressions written in index form.
CONTENTS

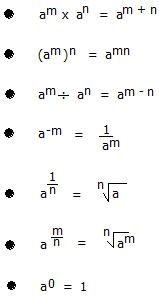
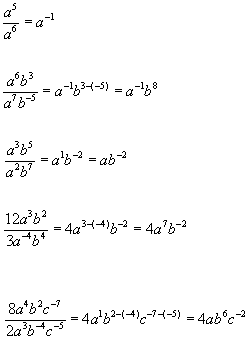
https://youtu.be/-zUmvpkhvW8
EVALUATION: New General Mathematics for JS2, Page25 Ex 2c, Questions 1a-e, 2a-e.
ASSIGNMENT: New General Mathematics for JS2, Page 25, Ex 2c, Questions 1f- j and 2 f- j.
further studies
Study More...
LESSON 31
TOPIC: Standard form
REFERENCE BOOK: New General Mathematics f or JS2.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express any whole number in standard form.
CONTENTS
Numbers in standard form are all in the form A +10n such that A is a number between 1 and 10 and n is a whole number.
Example: Express the following in standard form:
(a) 60000 = 6 + 104
(b) 480 000000 = 4.8 + 108
(c) 320 000 = 3.2 + 105
(d) 750 = 7.5 + 102
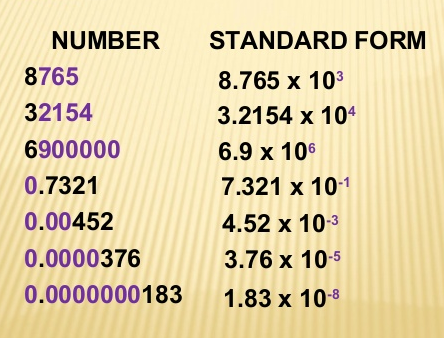
https://youtu.be/N6RjbBrQzbk
EVALUATION:
Express the following numbers in standard form:
(a) 9 000 000
(b) 4 000
(c) 4 000000000
(d) 600
(e) 8900
(f) 55
(g) 23 000000
(h) 34
ASSIGNMENT: Express the following numbers in standard form:
(a) 20 000 000
(b) 54 000
(c) 25 000 000
(d) 950
(e) 360
(f) 170 000
(g) 950
(h) 410 000
further studies
Study More...
practice test
Practice More...
LESSON 32
TOPIC: Expressing standard form in ordinary form.
REFERENCE BOOK: New General Mathematics for JS2, Page27.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express numbers written in standard form in ordinary form.
CONTENTS:
Example: Express the following in ordinary form:
(a) 4 x 104 = 4 + 10000 = 40 000
(b) 2.3 x 105 = 4.3 x 10 000 = 23 000
(c) 7.3 x 107 = 7.3 x 10 000 000 = 73 000 000
https://youtu.be/0mKwJPd2ZEs
EVALUATION: The lesson is evaluated from New General Mathematics for JS2, Page 27, Ex 2f, Questions 1- 5,and 10 -15.
ASSIGNMENT: New General Mathematics for JS2, Page 27, Ex 2f, Questions 6 - 10 and 16- 20.
practice test
Practice More...
LESSON 33
TOPIC: Expressing Decimal Fractions in Standard Form.
REFERENCE BOOK: New General Mathematics f or JS2,Page 27.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express decimal fractions in standard form.

CONTENTS
Express the following in standard form:
(a) 0.00007 = 7/100 000 = 7 /105 = 7 x 10-5
(b) 0.000 000 022 = 2.2/100 000 000 = 2.2 x 10-8
(c) 0.000 0063 = 6.3/1000 000 = 6.3 x 10-6


https://youtu.be/8bUvkPYXjco
EVALUATION: Express the following in standard form:
(a) 0.005
(b) 0.08
(c) 0.0006
(d) 0.000004
(e) 0.3
(f) 0.00088
(g) 0.000 0055
ASSIGNMENT: New General Mathematics for JS2, Page 27, Ex 2g, Questions 15 -24.
further studies
http://www.mathwarehouse.com/scientific_notation/
practice test
http://www.mathgoodies.com/lessons/deci ... write.html
LESSON 34
TOPIC: Expressing decimal standard form as decimal fractions.
REFERENCE BOOK: New General Mathematics for JS2, Page 28.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express decimal standard forms as decimal fractions.

CONTENTS
Example:
(a) 9 x 10-4 = 9/10 000 = 0.0009
(b) 5.2 x 10-5 = 5.2/100000 = 0.00052
(c) 3.4 x 102 = 3.4 x 100 = 340
(d) 7.8 x 102 = 7.8 100 =780
https://youtu.be/gvPI8YxhSok
EVALUATION The lesson is evaluated from New General Mathematics for JS2, Page 28, EX 2H, QUESTIONS 1- 5.
ASSIGNMENT New General Mathematics for JS2 Page 28, Ex 2h, questions 6- 12.
http://www.youtube.com/watch?v=naVTfgmiPUc
TOPIC STANDARD FORM (Laws of indices).
REFERENCE BOOK New General Mathematics for JS2, Page 23.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to, students should be able to simplify numbers and expressions written in index form.
CONTENTS

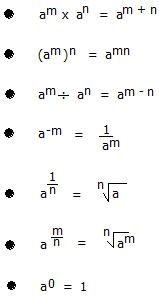
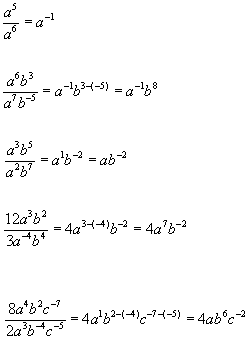
https://youtu.be/-zUmvpkhvW8
EVALUATION: New General Mathematics for JS2, Page25 Ex 2c, Questions 1a-e, 2a-e.
ASSIGNMENT: New General Mathematics for JS2, Page 25, Ex 2c, Questions 1f- j and 2 f- j.
further studies
Study More...
LESSON 31
TOPIC: Standard form
REFERENCE BOOK: New General Mathematics f or JS2.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express any whole number in standard form.
CONTENTS
Numbers in standard form are all in the form A +10n such that A is a number between 1 and 10 and n is a whole number.
Example: Express the following in standard form:
(a) 60000 = 6 + 104
(b) 480 000000 = 4.8 + 108
(c) 320 000 = 3.2 + 105
(d) 750 = 7.5 + 102

https://youtu.be/N6RjbBrQzbk
EVALUATION:
Express the following numbers in standard form:
(a) 9 000 000
(b) 4 000
(c) 4 000000000
(d) 600
(e) 8900
(f) 55
(g) 23 000000
(h) 34
ASSIGNMENT: Express the following numbers in standard form:
(a) 20 000 000
(b) 54 000
(c) 25 000 000
(d) 950
(e) 360
(f) 170 000
(g) 950
(h) 410 000
further studies
Study More...
practice test
Practice More...
LESSON 32
TOPIC: Expressing standard form in ordinary form.
REFERENCE BOOK: New General Mathematics for JS2, Page27.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express numbers written in standard form in ordinary form.

CONTENTS:
Example: Express the following in ordinary form:
(a) 4 x 104 = 4 + 10000 = 40 000
(b) 2.3 x 105 = 4.3 x 10 000 = 23 000
(c) 7.3 x 107 = 7.3 x 10 000 000 = 73 000 000
https://youtu.be/0mKwJPd2ZEs
EVALUATION: The lesson is evaluated from New General Mathematics for JS2, Page 27, Ex 2f, Questions 1- 5,and 10 -15.
ASSIGNMENT: New General Mathematics for JS2, Page 27, Ex 2f, Questions 6 - 10 and 16- 20.
practice test
Practice More...
LESSON 33
TOPIC: Expressing Decimal Fractions in Standard Form.
REFERENCE BOOK: New General Mathematics f or JS2,Page 27.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express decimal fractions in standard form.

CONTENTS
Express the following in standard form:
(a) 0.00007 = 7/100 000 = 7 /105 = 7 x 10-5
(b) 0.000 000 022 = 2.2/100 000 000 = 2.2 x 10-8
(c) 0.000 0063 = 6.3/1000 000 = 6.3 x 10-6


https://youtu.be/8bUvkPYXjco
EVALUATION: Express the following in standard form:
(a) 0.005
(b) 0.08
(c) 0.0006
(d) 0.000004
(e) 0.3
(f) 0.00088
(g) 0.000 0055
ASSIGNMENT: New General Mathematics for JS2, Page 27, Ex 2g, Questions 15 -24.
further studies
http://www.mathwarehouse.com/scientific_notation/
practice test
http://www.mathgoodies.com/lessons/deci ... write.html
LESSON 34
TOPIC: Expressing decimal standard form as decimal fractions.
REFERENCE BOOK: New General Mathematics for JS2, Page 28.
BEHAVIOURAL OBJECTIVES: At the end of this lesson, students should be able to express decimal standard forms as decimal fractions.

CONTENTS
Example:
(a) 9 x 10-4 = 9/10 000 = 0.0009
(b) 5.2 x 10-5 = 5.2/100000 = 0.00052
(c) 3.4 x 102 = 3.4 x 100 = 340
(d) 7.8 x 102 = 7.8 100 =780
https://youtu.be/gvPI8YxhSok
EVALUATION The lesson is evaluated from New General Mathematics for JS2, Page 28, EX 2H, QUESTIONS 1- 5.
ASSIGNMENT New General Mathematics for JS2 Page 28, Ex 2h, questions 6- 12.
http://www.youtube.com/watch?v=naVTfgmiPUc