SCHEME OF WORK
WEEK TOPICS
1. Revision of last term examination questions
Prime Numbers and Factors; Prime Numbers and Index Notation
2. Whole Numbers and Decimal Numbers: Whole numbers in standard form. Expression of decimal numbers in standard form. Prime factors of numbers not greater than 200. Perfect squares.
3. The least Common Multiples (LCM) of numbers. The Highest Common Factor (HCF) of numbers.
4. Square roots of perfect squares by factor method. Solving quantitative reasoning problems related to contents of week 2 and 3 above
5. Fractions: Expressing fractions as ratios, decimals and percentages (conversion of simple fractions to ratios, decimals and percentages).
6. Solving quantitative reasoning problems related to conversion of fractions to ratios, decimals and percentages.
7. Transactions in the Homes and Offices: Household Arithmetic, Commercial Arithmetic – solving problems relating to profit, interest, discount and commission. Value orientation.
8. Approximation: Approximation of numbers. Quantitative Reasoning – Solving quantitative reasoning problems related to approximation of numbers.
9. Multiplication and Division of directed numbers: Square and square root tables. Charts – Interpretation and use of tables, charts, records and schedules. Multiplication and Division of directed numbers.
10. Algebraic Expressions: Expansion of algebraic expressions. Factorization of simple algebraic expressions. Algebraic expressions of fractions with monomial denominations. Quantitative reasoning and the use of quadratic equation box in expanding and factorizing algebraic and factorizing algebraic expressions. Finding missing factors in a given expression.
11. Revision
1ST TERM
WEEK 1
LESSON 1
MAIN TOPIC: PRIME NUMBERS AND FACTORS
SPECIFIC TOPIC: PRIME NUMBERS
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to: (a) define a prime number (b) identify prime numbers by the use of the sieve of Eratosthenes method.
REFERENCE BOOK: MAN mathematics for bk 2, page 16

CONTENTS
Prime number: A prime number is a number that can only be divided by itself and 1 e.g. 2,3,5,7,11,13... 1 is not a prime number
The sieve of Eratosthenes

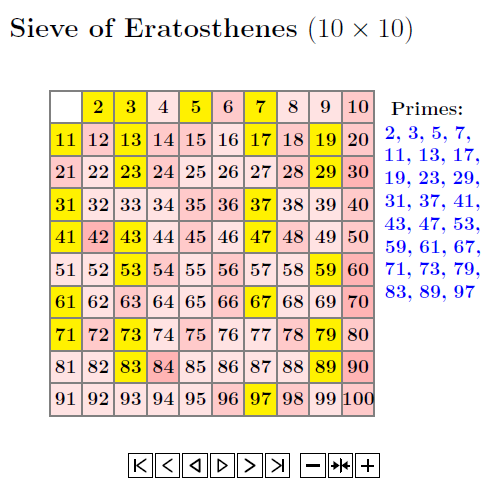
2 0 21
2 2 23 2 4 25
2 6 27
2 8 29
3 0 31 3 2 33
3 4 35 3 6 37 3 8 39
4 0 41 4 2 43 4 4 45
4 6 47 4 8 49
5 0 51 5 2 53 5 4 55
5 6
Example: use sieve of Eratosthenes to find the prime numbers between 20 and 56
(a) Cross out all number divisible by 2 except 2 itself
(b) Cross out all numbers divisible by 3 except 3 itself
(c) Cross out all numbers divisible by 5, except 5 itself
(d) Cross out all numbers divisible by 7, except 7 itself
Hence, the prime numbers between 20 and 56 are 23,29,31,41,43,47 and 53

EVALUATION
(a) What is a prime number?
(b) Use sieve of Eratosthenes to locate the prime numbers between 30 and 100.
HOMEWORK
Use sieve of Eratosthenes to locate the prime number, between 90 and 118
Sieve of Eratosthenes
Read More...
watch video
https://www.youtube.com/watch?v=9m2cdWorIq8
LESSON 2
TOPIC: FACTORS, PRIME FACTORS AND INDEX NOTATION
PERFORMANCE OBJECTIVES: At the end of this lesson, students should be able to: Find factors of given numbers
REFERENCE BOOK: NGM for JSS bk 2, page 13

CONTENTS
Factors: (i) Write down all the factors of 24
24 = 1 x 24
2 x 12
3 x 8
4 x 6
Factors of 24 are: 1,2,3,4,6,12 and 24
(ii) state all the factors of 100
100 = 1 x 100
2 x 50
4 x 25
5 x 20
:. Factors of 100 are: 1,2,4,5,20,25,50,100
EVALUATION
Write down all the factors of each of the following (a)18 (b)72 (c)50 (d)48 (e) 120
HOMEWORK: Write down the factors of: (a)63 (b)56 (c)30 (d)28 (e)22
watch video
https://youtu.be/XGbOiYhHY2c
LESSON 3
TOPIC: PRIME FACTORS
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to: find prime factors of numbers
REFERENCE BOOK: NGM for JSS 2, page 13

CONTENTS
(a) Find the prime factors of 30
30 = 1 x 30
2 x 15
3 x 10
5 x 6
Factors of 30 are: 1, 2,3,5,6,10,15,30
Prime factors are 2,3, and 5
(b) State the prime factors of 42
42 = 1 x 42
2 x 21
3 x 14
6 x 7
Factors are: 1, 2,3,6,7,14,21,42
Prime factors are: 2,3 and 7
EVALUATION: Find the prime factors of each of the following (a) 120 (b)100 (c) 84 (d) 60
further studies
Read More...
watch video
https://www.youtube.com/watch?v=3VflanaZ1Qc
LESSON 4
TOPIC: PRIME FACTORS (INDEX NOTATION)
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to express given numbers as product of their prime factors
REFERENCE BOOK: MAN mathematics for JSS page 17
CONTENTS
INDEX NOTATION
(a) Find the prime factors of 60 giving your answer in index form
2 60
2 30
3 15
5 5
1
60 = 2 x 2 x 3 x 5
= 22 x 3 x 5(index form)
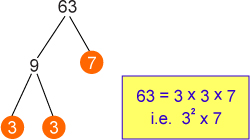
(b) Express 1800 as the product of prime factors using index notation
2 1800
2 900
2 450
3 225
3 75
5 25
5 5
1
1800 = 2 x 2 x 2 x 3 x 3 x 5 x 5
= 23 x 32 x 52

EVALUATION: Find the prime factors of each of the following using index notation (a) 720 (b) 1260 (c) 4800 (d) 360
HOMEWORK: Express in index form: (a) 6620 (b) 5420 (c) 840 (d) 80
LESSON 5
TOPIC: FACTORS, PRIME FACTORS AND INDEX NOTATION
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able : (i) find factors of number (ii) find prime factors of numbers (iii)express numbers as product of prime factors in index form
REFERENCE BOOK: (i) NGM for JSS 2, page 13 (ii) MAN mathematics for JSS2, page 16
CONTENTS
Questions (revision)
a. Write down all the factors of 400
400 = 1 x 400
2 x 200
4 x 100
5 x 80
10 x 40
8 x 50
Factors are: 1,2,4,5,8,`0,40,50,80,100,200,400
b. Find the prime factors of 108
108 = 1 x 108
2 x 54
3 x 36
4 x 27
9 x 12
Factors are: 1, 2,3,4,9,12,27,36,54,108
Prime factors are: 2 and 3
c. Express 8 as a product of its prime factors in index form
2 88
2 44
2 22
11 11
1

EVALUATION
(a) Write down all the factors of 150
(b) Find the prime factors of 45
(c)Express 1260 as a product of its prime factors in index form
HOMEWORK
(a) Which is larger? (i) 63 or 36 (ii) 28 or 82
(b) Find the product if the third power of 3 and the second power of 2
(c) Simplify : 72 x 62 x 53
152 x 22
further studies
Read More...
watch videos
https://youtu.be/FyVXSIGqywg
https://youtu.be/k85IhfyP-po
MAIN TOPIC: PRIME NUMBERS AND FACTORS
SPECIFIC TOPIC: PRIME NUMBERS
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to: (a) define a prime number (b) identify prime numbers by the use of the sieve of Eratosthenes method.
REFERENCE BOOK: MAN mathematics for bk 2, page 16

CONTENTS
Prime number: A prime number is a number that can only be divided by itself and 1 e.g. 2,3,5,7,11,13... 1 is not a prime number
The sieve of Eratosthenes


2 0 21
2 2 23 2 4 25
2 6 27
2 8 29
3 0 31 3 2 33
3 4 35 3 6 37 3 8 39
4 0 41 4 2 43 4 4 45
4 6 47 4 8 49
5 0 51 5 2 53 5 4 55
5 6
Example: use sieve of Eratosthenes to find the prime numbers between 20 and 56
(a) Cross out all number divisible by 2 except 2 itself
(b) Cross out all numbers divisible by 3 except 3 itself
(c) Cross out all numbers divisible by 5, except 5 itself
(d) Cross out all numbers divisible by 7, except 7 itself
Hence, the prime numbers between 20 and 56 are 23,29,31,41,43,47 and 53

EVALUATION
(a) What is a prime number?
(b) Use sieve of Eratosthenes to locate the prime numbers between 30 and 100.
HOMEWORK
Use sieve of Eratosthenes to locate the prime number, between 90 and 118
Sieve of Eratosthenes
Read More...
watch video
https://www.youtube.com/watch?v=9m2cdWorIq8
LESSON 2
TOPIC: FACTORS, PRIME FACTORS AND INDEX NOTATION
PERFORMANCE OBJECTIVES: At the end of this lesson, students should be able to: Find factors of given numbers
REFERENCE BOOK: NGM for JSS bk 2, page 13

CONTENTS
Factors: (i) Write down all the factors of 24
24 = 1 x 24
2 x 12
3 x 8
4 x 6
Factors of 24 are: 1,2,3,4,6,12 and 24
(ii) state all the factors of 100
100 = 1 x 100
2 x 50
4 x 25
5 x 20
:. Factors of 100 are: 1,2,4,5,20,25,50,100
EVALUATION
Write down all the factors of each of the following (a)18 (b)72 (c)50 (d)48 (e) 120
HOMEWORK: Write down the factors of: (a)63 (b)56 (c)30 (d)28 (e)22
watch video
https://youtu.be/XGbOiYhHY2c
LESSON 3
TOPIC: PRIME FACTORS
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to: find prime factors of numbers
REFERENCE BOOK: NGM for JSS 2, page 13

CONTENTS
(a) Find the prime factors of 30
30 = 1 x 30
2 x 15
3 x 10
5 x 6
Factors of 30 are: 1, 2,3,5,6,10,15,30
Prime factors are 2,3, and 5
(b) State the prime factors of 42
42 = 1 x 42
2 x 21
3 x 14
6 x 7
Factors are: 1, 2,3,6,7,14,21,42
Prime factors are: 2,3 and 7
EVALUATION: Find the prime factors of each of the following (a) 120 (b)100 (c) 84 (d) 60
further studies
Read More...
watch video
https://www.youtube.com/watch?v=3VflanaZ1Qc
LESSON 4
TOPIC: PRIME FACTORS (INDEX NOTATION)
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to express given numbers as product of their prime factors
REFERENCE BOOK: MAN mathematics for JSS page 17
CONTENTS
INDEX NOTATION
(a) Find the prime factors of 60 giving your answer in index form
2 60
2 30
3 15
5 5
1
60 = 2 x 2 x 3 x 5
= 22 x 3 x 5(index form)
(b) Express 1800 as the product of prime factors using index notation
2 1800
2 900
2 450
3 225
3 75
5 25
5 5
1
1800 = 2 x 2 x 2 x 3 x 3 x 5 x 5
= 23 x 32 x 52


EVALUATION: Find the prime factors of each of the following using index notation (a) 720 (b) 1260 (c) 4800 (d) 360
HOMEWORK: Express in index form: (a) 6620 (b) 5420 (c) 840 (d) 80
LESSON 5
TOPIC: FACTORS, PRIME FACTORS AND INDEX NOTATION
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able : (i) find factors of number (ii) find prime factors of numbers (iii)express numbers as product of prime factors in index form
REFERENCE BOOK: (i) NGM for JSS 2, page 13 (ii) MAN mathematics for JSS2, page 16
CONTENTS
Questions (revision)
a. Write down all the factors of 400
400 = 1 x 400
2 x 200
4 x 100
5 x 80
10 x 40
8 x 50
Factors are: 1,2,4,5,8,`0,40,50,80,100,200,400
b. Find the prime factors of 108
108 = 1 x 108
2 x 54
3 x 36
4 x 27
9 x 12
Factors are: 1, 2,3,4,9,12,27,36,54,108
Prime factors are: 2 and 3
c. Express 8 as a product of its prime factors in index form
2 88
2 44
2 22
11 11
1

EVALUATION
(a) Write down all the factors of 150
(b) Find the prime factors of 45
(c)Express 1260 as a product of its prime factors in index form
HOMEWORK
(a) Which is larger? (i) 63 or 36 (ii) 28 or 82
(b) Find the product if the third power of 3 and the second power of 2
(c) Simplify : 72 x 62 x 53
152 x 22
further studies
Read More...
watch videos
https://youtu.be/FyVXSIGqywg
https://youtu.be/k85IhfyP-po
WEEK 2
LESSON 6
TOPIC: Whole Numbers and Decimal Numbers
CONTENT:
Whole numbers in standard form.
Expression of decimal numbers in standard form.
Prime factors of numbers not greater than 200.
Perfect squares
WHOLE NUMBERS IN STANDARD FORM
A number is said to be in standard form if it is expressed in the form of A x 10n. Where 1<A<10 and n is an integer (positive or negative whole numbers). Standard form is very useful in field of sciences and social sciences for easy presentations and analysis. Examples of numbers in standard form includes: 4 x 109, 5.8 x 102, 5.62 x 104 , etc
Examples:
1. Write the following in standard form:
(a)90 000 000 (b). 6 000 000 000 000 000 000 (c). 34256.189 (d). 879.45
Solutions:
(a). 90 000 000 = 9 X 10 000 000 = 9 X 10 X 10 X 10 X 10 X10 X 10 X 10 = 9 x 107
(b). 6 X 1000 000 000 000 000 000 = 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 = 6 X 1018
(c). 34256.189 = 3.4256189 X 10 000 = 3.4256189 X 104
(d). 879.45 = 8.7945 X 100 = 8.7945 10 X 10 = 8.7945 X 102
2. Express each of the following in ordinary forms or full figures:
(a). 7.879 x 105 (b). 6.209 x 104 (c). 4.231 x 106
Solutions:
(a). 7.879 x 105 = 7.879 x 10 x 10 x 10 x 10 x 10 = 7.879 x 100 000 = 787900
(b). 6.209 x 104 = 6.209 x 10 x 10 x 10 x 10 = 6.209 x 10 000 = 6.2090
(c). 4.231 x 106 = 4.231 x 10 x 10 x 10 x 10 x 10 x 10 = 4.231 x 1 000 000 = 4.2310000

Watch Video
https://youtu.be/BGiYOemaBRc
EXPRESSING DECIMAL NUMBERS IN STANDARD FORM.
Decimal fractions can be expressed in standard form using negative powers of ten (10). This means that, the values of n when a decimal number is expressed in standard forms are negative. To do this, we move the decimal point to Right Hand Side (RHS) in tenth.
Examples:
Express each of these numbers in standard form. 104
(a). 0.0008 (b). 0.0000 000 7 (c). 0. 000 036
Solutions:
(a). 0.0008 = 8÷10000=8/10000=8/(10 x 10 x 10 x 10)=8 x 1/104 = 8 x 10-4
(b). 0.000 00 7 = 7 ÷1000 000=7/1000000= 7 x 1/10 x 10 x 10 x 10 x 10 x 10 = 7 x 10-6
(c). 0. 000 036 = 36 ÷ 100000 = 36/100000= 36 x 1/ 10 x 10 x 10 x 10 x 10 x 10 = 3.6 x 106
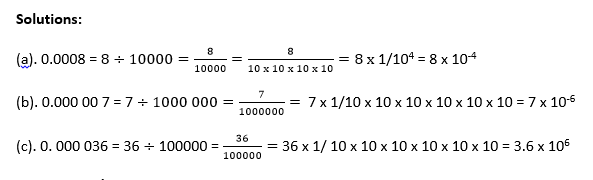
More examples:
Write the following as decimal fractions and standard forms:
16 thousandths (b) 60 millionths
Solutions:
16 thousandths = 1 thousandth x 16 = 0.001 x 16 = 0.0016
In standard form: 0.0016 = 1.6 x 10-3
60 millionths = 1 millionth x 60 = 0.00000 x 60 = 6 x 10-5
https://youtu.be/bXkewQ7WEdI
EVALUATION:
Express the following numbers in standard forms
50130002 (b) 0.0000032901 (c) 3518 x 1000000
(d) 0.000400254 (e) 0.000000000235 ÷1000000
Rewrite each of the following in ordinary forms
5.00009 x 105 (b) 8.543 x 10-4 (c) 6.653 x 10-6
Rewrite each of the following numbers in figures and put them in standard forms.
7 thousands (b) two and one quarter billion (c) 35 thousandths (d) 783 millionths
Further Studies
Read More...
Read More...
Read More...
Prime factors of numbers not greater than 200.
Prime factors of a number are the factors of the numbers which are not divisible by any other number except themselves and 1. For example the prime factors of 30 are 2,3 and 5, because out of all the factors of 30 (1,2,3,5,6,10,15 and 30), it is only 2,3 and 5 that are not divisible by any other number except themselves and 1.
Examples:
Write the factors of the following numbers and state the prime factors, hence express each number as a product of its prime factors.
(a) 22 (b) 50 (c) 63 (d) 42
Solutions:
22
Factors of 22 are 1, 2, 11, 22
The prime factors of 22 are 2 and 11
Product of its prime factors of 22 = 2 x11
50
Factors of 50 are 1, 2, 5, 10, 25 and 50
The prime factors of 50 are 2 and 5
Product of its prime factors of 50 = 2 x 5 x 5 = 2 x 52
63
Factors of 63 are 1, 3, 7, 9, 21 and 63
The prime factors of 63 are 3 and 7
Product of its prime factors of 63 = 3 x 3 x 7 = 32 x 7
42
Factors of 42 are 1, 2, 3, 6, 7, 14, 21 and 42
The prime factors of 42 are 2, 3 and 7
Product of its prime factors of 42 = 2 x 3 x 7

More examples:
Express (a) 27 (b) 104 (c) 116 as products of their prime factors in index form.
Solutions:
Divide each of the numbers by the prime factors in turns until it will not divide any further.
27
3 27
3 9
3 3
1
∴27 = 3 x 3 x 3 = 33
104
2 104
2 52
2 26
13 13
1
∴104= 2 x 2 x 2 x 13 = 23 x 13
116
2 116
2 58
29 29
1
∴116=2 x 2 x 29 = 22 x 29

EVALUATION:
For each of the following numbers: 39, 53, 72 and 56
Write their factors (b) state which factors are prime numbers
(c)Express the numbers as product of its prime factors
2. Show that 61 is a prime number
3. Express each number as a product of its prime factors in index form: 117, 200, 98, 52 and 174
https://youtu.be/-RhdzNYfF-M
LESSON 7
SQUARES AND PERFECT SQUARES:
A square of a number is any number that is multiplied by it-self. Examples include 2 x 2, a x a, 24 x 24, etc
A perfect square is a whole number whose square root is also a whole number. Perfect squares are simply squares of the form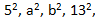 etc.
etc.
Examples:
16 = 4 x 4 here 16 is a perfect square since it can be express as 4 x 4
152 = 15 x 15 = 225 and so 255 is a perfect square.
702 = 70 x 70 = 4 900 is a perfect square.
162 = 16 x 16 = 256, so 256 is a perfect square.
Hence any number multiplied by it-self gives a perfect square.
For example:
9 = 3 x 3 and √9=3
25 = 5 x 5 and √25 = 5
225 = 3 x 3 x 5 x 5 and √225 =15
64 = 2 x 2 x 2 x 2 x 2 x 2 and √64 = 8
100 = 2 x 2 x 5 x 5 and √100 = 10
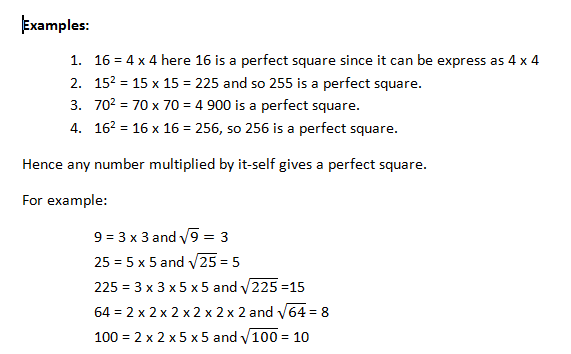
This implies that 9, 25, 225, 64 and 100 are perfect squares because their square roots are whole numbers.
It is always possible to express a perfect square in factors with even indices. For example: 9216 =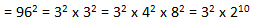
Example:
Find the smallest number by which 540 must be multiplied so that the product is a perfect square.
Solution:
2 540
2 270
3 135
3 45
3 15
5 5
1
540 = 22 x 33 x 5.

The index (power) of 2 is even. The indices of 3 and 5 are odd. One more 3 and one more 5 will then be a perfect square.
The number required = 3 x 5 = 15
https://www.youtube.com/watch?v=B-Sfvry_h3Q
EVALUATION:
Identify perfect squares from the following numbers:
169, 440, 7200, 1600, 310 , 440, 10000, 625
Find the smallest number that must be added to each of the following numbers to make the number a perfect square:
99, 288, 405, 162, 243, 361
Find the square of each of the following:
95, 21, 34, 28, 17, 13, 336
Find the numbers whose squares are:
81, 400, 1600, 1089, 256, 729
ASSIGNMENT:
New General Mathematics for JSS 1 (UBE Edition) pages 20 to 21
New General Mathematics for JSS 1 (UBE Edition) pages 21: Ex. 1j: Q1 to Q13
Read More...
TOPIC: Whole Numbers and Decimal Numbers
CONTENT:
Whole numbers in standard form.
Expression of decimal numbers in standard form.
Prime factors of numbers not greater than 200.
Perfect squares
WHOLE NUMBERS IN STANDARD FORM
A number is said to be in standard form if it is expressed in the form of A x 10n. Where 1<A<10 and n is an integer (positive or negative whole numbers). Standard form is very useful in field of sciences and social sciences for easy presentations and analysis. Examples of numbers in standard form includes: 4 x 109, 5.8 x 102, 5.62 x 104 , etc
Examples:
1. Write the following in standard form:
(a)90 000 000 (b). 6 000 000 000 000 000 000 (c). 34256.189 (d). 879.45
Solutions:
(a). 90 000 000 = 9 X 10 000 000 = 9 X 10 X 10 X 10 X 10 X10 X 10 X 10 = 9 x 107
(b). 6 X 1000 000 000 000 000 000 = 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 X 10 = 6 X 1018
(c). 34256.189 = 3.4256189 X 10 000 = 3.4256189 X 104
(d). 879.45 = 8.7945 X 100 = 8.7945 10 X 10 = 8.7945 X 102
2. Express each of the following in ordinary forms or full figures:
(a). 7.879 x 105 (b). 6.209 x 104 (c). 4.231 x 106
Solutions:
(a). 7.879 x 105 = 7.879 x 10 x 10 x 10 x 10 x 10 = 7.879 x 100 000 = 787900
(b). 6.209 x 104 = 6.209 x 10 x 10 x 10 x 10 = 6.209 x 10 000 = 6.2090
(c). 4.231 x 106 = 4.231 x 10 x 10 x 10 x 10 x 10 x 10 = 4.231 x 1 000 000 = 4.2310000

Watch Video
https://youtu.be/BGiYOemaBRc
EXPRESSING DECIMAL NUMBERS IN STANDARD FORM.
Decimal fractions can be expressed in standard form using negative powers of ten (10). This means that, the values of n when a decimal number is expressed in standard forms are negative. To do this, we move the decimal point to Right Hand Side (RHS) in tenth.
Examples:
Express each of these numbers in standard form. 104
(a). 0.0008 (b). 0.0000 000 7 (c). 0. 000 036
Solutions:
(a). 0.0008 = 8÷10000=8/10000=8/(10 x 10 x 10 x 10)=8 x 1/104 = 8 x 10-4
(b). 0.000 00 7 = 7 ÷1000 000=7/1000000= 7 x 1/10 x 10 x 10 x 10 x 10 x 10 = 7 x 10-6
(c). 0. 000 036 = 36 ÷ 100000 = 36/100000= 36 x 1/ 10 x 10 x 10 x 10 x 10 x 10 = 3.6 x 106
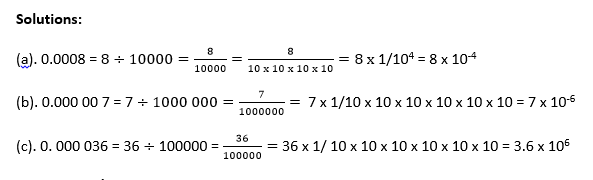
More examples:
Write the following as decimal fractions and standard forms:
16 thousandths (b) 60 millionths
Solutions:
16 thousandths = 1 thousandth x 16 = 0.001 x 16 = 0.0016
In standard form: 0.0016 = 1.6 x 10-3
60 millionths = 1 millionth x 60 = 0.00000 x 60 = 6 x 10-5
https://youtu.be/bXkewQ7WEdI
EVALUATION:
Express the following numbers in standard forms
50130002 (b) 0.0000032901 (c) 3518 x 1000000
(d) 0.000400254 (e) 0.000000000235 ÷1000000
Rewrite each of the following in ordinary forms
5.00009 x 105 (b) 8.543 x 10-4 (c) 6.653 x 10-6
Rewrite each of the following numbers in figures and put them in standard forms.
7 thousands (b) two and one quarter billion (c) 35 thousandths (d) 783 millionths
Further Studies
Read More...
Read More...
Read More...
Prime factors of numbers not greater than 200.
Prime factors of a number are the factors of the numbers which are not divisible by any other number except themselves and 1. For example the prime factors of 30 are 2,3 and 5, because out of all the factors of 30 (1,2,3,5,6,10,15 and 30), it is only 2,3 and 5 that are not divisible by any other number except themselves and 1.
Examples:
Write the factors of the following numbers and state the prime factors, hence express each number as a product of its prime factors.
(a) 22 (b) 50 (c) 63 (d) 42
Solutions:
22
Factors of 22 are 1, 2, 11, 22
The prime factors of 22 are 2 and 11
Product of its prime factors of 22 = 2 x11
50
Factors of 50 are 1, 2, 5, 10, 25 and 50
The prime factors of 50 are 2 and 5
Product of its prime factors of 50 = 2 x 5 x 5 = 2 x 52
63
Factors of 63 are 1, 3, 7, 9, 21 and 63
The prime factors of 63 are 3 and 7
Product of its prime factors of 63 = 3 x 3 x 7 = 32 x 7
42
Factors of 42 are 1, 2, 3, 6, 7, 14, 21 and 42
The prime factors of 42 are 2, 3 and 7
Product of its prime factors of 42 = 2 x 3 x 7

More examples:
Express (a) 27 (b) 104 (c) 116 as products of their prime factors in index form.
Solutions:
Divide each of the numbers by the prime factors in turns until it will not divide any further.
27
3 27
3 9
3 3
1
∴27 = 3 x 3 x 3 = 33
104
2 104
2 52
2 26
13 13
1
∴104= 2 x 2 x 2 x 13 = 23 x 13
116
2 116
2 58
29 29
1
∴116=2 x 2 x 29 = 22 x 29

EVALUATION:
For each of the following numbers: 39, 53, 72 and 56
Write their factors (b) state which factors are prime numbers
(c)Express the numbers as product of its prime factors
2. Show that 61 is a prime number
3. Express each number as a product of its prime factors in index form: 117, 200, 98, 52 and 174
https://youtu.be/-RhdzNYfF-M
LESSON 7
SQUARES AND PERFECT SQUARES:
A square of a number is any number that is multiplied by it-self. Examples include 2 x 2, a x a, 24 x 24, etc
A perfect square is a whole number whose square root is also a whole number. Perfect squares are simply squares of the form
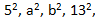 etc.
etc.Examples:
16 = 4 x 4 here 16 is a perfect square since it can be express as 4 x 4
152 = 15 x 15 = 225 and so 255 is a perfect square.
702 = 70 x 70 = 4 900 is a perfect square.
162 = 16 x 16 = 256, so 256 is a perfect square.
Hence any number multiplied by it-self gives a perfect square.
For example:
9 = 3 x 3 and √9=3
25 = 5 x 5 and √25 = 5
225 = 3 x 3 x 5 x 5 and √225 =15
64 = 2 x 2 x 2 x 2 x 2 x 2 and √64 = 8
100 = 2 x 2 x 5 x 5 and √100 = 10
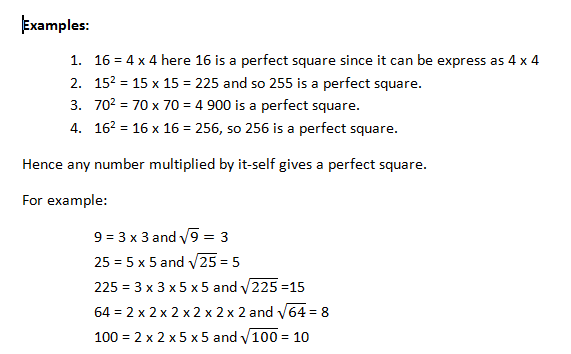
This implies that 9, 25, 225, 64 and 100 are perfect squares because their square roots are whole numbers.
It is always possible to express a perfect square in factors with even indices. For example: 9216 =
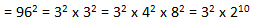
Example:
Find the smallest number by which 540 must be multiplied so that the product is a perfect square.
Solution:
2 540
2 270
3 135
3 45
3 15
5 5
1
540 = 22 x 33 x 5.

The index (power) of 2 is even. The indices of 3 and 5 are odd. One more 3 and one more 5 will then be a perfect square.
The number required = 3 x 5 = 15
https://www.youtube.com/watch?v=B-Sfvry_h3Q
EVALUATION:
Identify perfect squares from the following numbers:
169, 440, 7200, 1600, 310 , 440, 10000, 625
Find the smallest number that must be added to each of the following numbers to make the number a perfect square:
99, 288, 405, 162, 243, 361
Find the square of each of the following:
95, 21, 34, 28, 17, 13, 336
Find the numbers whose squares are:
81, 400, 1600, 1089, 256, 729
ASSIGNMENT:
New General Mathematics for JSS 1 (UBE Edition) pages 20 to 21
New General Mathematics for JSS 1 (UBE Edition) pages 21: Ex. 1j: Q1 to Q13
Read More...
WEEK 3
LESSON 8
TOPIC: Square of whole numbers
REFERENCE BOOK: MAN Mathematics for JSS 2, page 18
BEHAVIORAL OBJECTIVE: At the end of the lesson, student should be able to:
(i) find the square of whole numbers
(ii) Find the square of decimal fractions

CONTENT
Square of whole numbers
82 = 8 X 8 = 68
212 = 21 X 21 = 441
152 = 15 X 15 = 225
402 = 40 X 40 = 1600
Difference of two squares
Examples: 15 - 12
= (15+12)(15-12)
= (27) (3)
= 81
Read More...
Square of decimal numbers.
(i) (0.5) 2 = 0.5 X 0.5
= 0.25
(ii) (0.09) 2 = 0.09 X 0.09
Read More...
EVALUATION: find the square of each of the following
(a) 24 (b) 13 (c) 0.11 (d) 0.04
EVALUATE: 672 - 332
ASSIGNMENT:
Find the square of each of the following (a) 91 (b) 5.5 (c) 101
Evaluate: 452 - 152
LESSON 9
TOPIC: PERFECT SQUARE
REFERENCE BOOK: MAN Mathematics for JSS 2, page 18
BEHAVIORAL OBJECTIVE: At the end of the lesson, student should be able to: determine the conditions for a number to be transformed into a perfect square.

CONTENT
A perfect square is the result got when a whole number is multiplied by itself.
Example: 1 X 1 = 1
2 X 2 = 4
3 X 3 = 9
4 X 4 = 16
Thus, 1,4,9,16.... Are all perfect squares.
Example 1: Find the smallest number by which 50 will be multiplied so that the product is a perfect square.
2 50
5 25
5 5
1 1
50 = 2 X 5 X 5.
The index of 2 is 1. It must be even i.e 2 or 4....
Therefore there is need for at least one more 2 to make the index of 2 even
;. The least number required is 2
50 X 2 = 2 X 2 X 5 X 5
= 22 X 52
= 100
;. The number required is 2

EVALUATION
Find the smallest number by which each of the following will be multiplied so that the product is a perfect square.
(a) 20 (b) 504 (c) 147 (d) 13
ASSIGNMENT:
Make each number a perfect square by multiplying with the smallest number (a) 61 (b) 252 (c) 99 (d) 20
further studies
Read More...
practice test
Short Practice Test
LESSON 10
TOPIC: SQUARE ROOTS OF WHOLE NUMBERS
REFERENCE BOOK: MAN Mathematics for JSS 2, page 20
BEHAVIORAL OBJECTIVE: At the end of the lesson, student should be able to: calculate the square root of whole numbers.

CONTENT
Examples: Find the square root of 11025

EVALUATION: find the smallest number by which each of the following will be multiplied so that the product is a perfect square.
(a) 20 (b) 504 (c) 147 (d) 13
ASSIGNMENT:
Make each number a perfect square by multiplying with the smallest number
(a) 61 (b) 252 (c) 99 (d) 20
=
3. 11025
3. 3675
5. 1225
5. 245
7. 49
7. 7
1
11025 = 32 X 52 X 72
= 3 X 5 X 7
= 105
(ii) Find
2. 6400
2. 3200
2. 1600
2. 800
2. 400
2. 200
2. 100
2. 50
5. 25
5. 5
1
6400 = 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 5 X 5
= 22 X 22 X 22 X 52
= 2 X 2 X 2 X 2 X 5
= 80
https://www.youtube.com/watch?v=B4zejSI8zho&t=506s
FIND THE SQUARE ROOT OF (A) 225 (B) 441 (C) 1225 (D) 4900
ASSIGNMENT: FIND THE SQUARE ROOT OF (A) 784 (B) 484 (C) 900 (D) 324
further studies
Read More...
Read More...
Read More...
practice test
Short Practice Test
LESSON 11
TOPIC: SQUARE ROOTS OF DECIMAL FRACTION
REFERENCE BOOK: NEW GENERAL MATHEMATICS FOR JSS 2, PAGE 20
BEHAVIORAL OBJECTIVE: at the end of the lesson, student should be able to: find the square root of decimal fraction.

View Content 1 below
Difference-of-Two-Squares-and-Perfect-Squares-Trinomials2

(ii) Find the square root of 7.84
(iii) Find the square root of 61/4
https://youtu.be/2mejAHKMBiM
EVALUATION: find the smallest square root of (a) 0.01 (b) 70.56 (c) 4.48
ASSIGNMENT:
Find the square root of (a) 3.14 (b)77.44 (c) 0.81 (d) 19.36
further studies
Read More...
Read More...
LESSON 12
TOPIC: PERFECT OR SQUARE ROOT (REVISION
REFERENCE BOOK: New General Mathematics for JSS 2, page 20
BEHAVIORAL OBJECTIVE: At the end of the lesson, student should be able to: (i) determine the conditions necessary for making numbers perfect squares
(ii) Find the square root of numbers
(iii) Calculate the square of whole and decimal numbers
View Content 2 below

(a) Find the square of 35
i.e 352 = 35 X 35
= 1225
(b) Evaluate
= = 28
(c) Find the smallest numbers by which 72 will be multiplied in other to make it perfect square
72 = 2 X 2 X 2 X 3 X 3
= 23 X 32
= 23 X (2) X 32
;. Ans = 72 X 2 = 144
Ans. = 2
EVALUATION:
Find the smallest number by which 150 will be multiplied to make it perfect square.
ASSIGNMENT:
New General Maths for JSS 2, Page 21. Ex. 1K; 10 - 15
further studies
http://www.youtube.com/watch?v=Thxzb35HQlw
practice test
Short Practice Test
Short Practice Test
TOPIC: Square of whole numbers
REFERENCE BOOK: MAN Mathematics for JSS 2, page 18
BEHAVIORAL OBJECTIVE: At the end of the lesson, student should be able to:
(i) find the square of whole numbers
(ii) Find the square of decimal fractions


CONTENT
Square of whole numbers
82 = 8 X 8 = 68
212 = 21 X 21 = 441
152 = 15 X 15 = 225
402 = 40 X 40 = 1600
Difference of two squares

Examples: 15 - 12
= (15+12)(15-12)
= (27) (3)
= 81
Read More...
Square of decimal numbers.
(i) (0.5) 2 = 0.5 X 0.5
= 0.25
(ii) (0.09) 2 = 0.09 X 0.09
Read More...
EVALUATION: find the square of each of the following
(a) 24 (b) 13 (c) 0.11 (d) 0.04
EVALUATE: 672 - 332
ASSIGNMENT:
Find the square of each of the following (a) 91 (b) 5.5 (c) 101
Evaluate: 452 - 152
LESSON 9
TOPIC: PERFECT SQUARE
REFERENCE BOOK: MAN Mathematics for JSS 2, page 18
BEHAVIORAL OBJECTIVE: At the end of the lesson, student should be able to: determine the conditions for a number to be transformed into a perfect square.

CONTENT
A perfect square is the result got when a whole number is multiplied by itself.
Example: 1 X 1 = 1
2 X 2 = 4
3 X 3 = 9
4 X 4 = 16
Thus, 1,4,9,16.... Are all perfect squares.
Example 1: Find the smallest number by which 50 will be multiplied so that the product is a perfect square.
2 50
5 25
5 5
1 1
50 = 2 X 5 X 5.
The index of 2 is 1. It must be even i.e 2 or 4....
Therefore there is need for at least one more 2 to make the index of 2 even
;. The least number required is 2
50 X 2 = 2 X 2 X 5 X 5
= 22 X 52
= 100
;. The number required is 2

EVALUATION
Find the smallest number by which each of the following will be multiplied so that the product is a perfect square.
(a) 20 (b) 504 (c) 147 (d) 13
ASSIGNMENT:
Make each number a perfect square by multiplying with the smallest number (a) 61 (b) 252 (c) 99 (d) 20
further studies
Read More...
practice test
Short Practice Test
LESSON 10
TOPIC: SQUARE ROOTS OF WHOLE NUMBERS
REFERENCE BOOK: MAN Mathematics for JSS 2, page 20
BEHAVIORAL OBJECTIVE: At the end of the lesson, student should be able to: calculate the square root of whole numbers.

CONTENT
Examples: Find the square root of 11025

EVALUATION: find the smallest number by which each of the following will be multiplied so that the product is a perfect square.
(a) 20 (b) 504 (c) 147 (d) 13
ASSIGNMENT:
Make each number a perfect square by multiplying with the smallest number
(a) 61 (b) 252 (c) 99 (d) 20
=
3. 11025
3. 3675
5. 1225
5. 245
7. 49
7. 7
1
11025 = 32 X 52 X 72
= 3 X 5 X 7
= 105
(ii) Find
2. 6400
2. 3200
2. 1600
2. 800
2. 400
2. 200
2. 100
2. 50
5. 25
5. 5
1
6400 = 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 5 X 5
= 22 X 22 X 22 X 52
= 2 X 2 X 2 X 2 X 5
= 80
https://www.youtube.com/watch?v=B4zejSI8zho&t=506s
FIND THE SQUARE ROOT OF (A) 225 (B) 441 (C) 1225 (D) 4900
ASSIGNMENT: FIND THE SQUARE ROOT OF (A) 784 (B) 484 (C) 900 (D) 324
further studies
Read More...
Read More...
Read More...
practice test
Short Practice Test
LESSON 11
TOPIC: SQUARE ROOTS OF DECIMAL FRACTION
REFERENCE BOOK: NEW GENERAL MATHEMATICS FOR JSS 2, PAGE 20
BEHAVIORAL OBJECTIVE: at the end of the lesson, student should be able to: find the square root of decimal fraction.

View Content 1 below
Difference-of-Two-Squares-and-Perfect-Squares-Trinomials2

(ii) Find the square root of 7.84
(iii) Find the square root of 61/4
https://youtu.be/2mejAHKMBiM
EVALUATION: find the smallest square root of (a) 0.01 (b) 70.56 (c) 4.48
ASSIGNMENT:
Find the square root of (a) 3.14 (b)77.44 (c) 0.81 (d) 19.36
further studies
Read More...
Read More...
LESSON 12
TOPIC: PERFECT OR SQUARE ROOT (REVISION
REFERENCE BOOK: New General Mathematics for JSS 2, page 20
BEHAVIORAL OBJECTIVE: At the end of the lesson, student should be able to: (i) determine the conditions necessary for making numbers perfect squares
(ii) Find the square root of numbers
(iii) Calculate the square of whole and decimal numbers
View Content 2 below

(a) Find the square of 35
i.e 352 = 35 X 35
= 1225
(b) Evaluate
= = 28
(c) Find the smallest numbers by which 72 will be multiplied in other to make it perfect square
72 = 2 X 2 X 2 X 3 X 3
= 23 X 32
= 23 X (2) X 32
;. Ans = 72 X 2 = 144
Ans. = 2
EVALUATION:
Find the smallest number by which 150 will be multiplied to make it perfect square.
ASSIGNMENT:
New General Maths for JSS 2, Page 21. Ex. 1K; 10 - 15
further studies
http://www.youtube.com/watch?v=Thxzb35HQlw
practice test
Short Practice Test
Short Practice Test
WEEK 4
LESSON 13
TOPIC: LCM, HCF & Square Root of Perfect Squares by Factors
CONTENT:
The least Common Multiples (LCM) of numbers
The Highest Common Factor (HCF) of numbers.
Square roots of perfect squares by factor method.
quantitative reasoning problems on whole number, LCM, HCF and Square root of perfect square
The least Common Multiples (LCM) of numbers
The LCM of two or more quantities is the smallest common multiple they have.
For example:
The multiple of 2: 2, 4, 6, 8, 10, 12…
The multiple of 3: 3, 6, 9, 12, 15…
Notice that 6 and 12 are the common multiples of 2 & 3
But the Least Common multiple (LCM) is 6.
Example 1
Find the LCM of 22, 30 and 40
Method: express each number as a product of its prime factors.
22 = 2 x 11
30 = 2 x 3 x 5
40 = 2 x 2 x 2 x5 = 23 x 5
The prime factors of 22, 30 and 40 are 2, 3, 5, and 11.
The highest power of each prime factor must be in the LCM.
These are 23, 3, 5 and 11
Thus, LCM = 23 X 3 X 5 X 11
= 8 X 3 X 5 X 11
= 1320
Alternative method
2 22 30 40
2 11 15 20
2 11 15 10
3 11 15 5
5 11 5 5
11 11 1 1
1 1 1
Thus, LCM = 23 X 3 X 5 X 11 = 1320

EVALUATION
Find the LCM of the following:
18, 30 and 48
8, 10 and 12
Further Studies
Read More...
LESSON 14
The Highest Common Factor (HCF) of numbers
14 is the highest common factor (HCF) of 28 and 42. It is the greatest number which will divide exactly into both 28 and 42.
Example 1
Find the HCF of 504 and 588.
Method: express each number as a product of its prime factors.
2 504 2 588
2 252 2 294
2 126 3 147
3 63 7 49
3 21 7 7
7 7 1
1
504 = 23 x 32 x 7 588 = 22 x 3 x 72
Find the common prime factors
504 = (22 x 3 x 7) x 2 x 3
588 = (22 x 3 x 7) x 7
The HCF is the product of the common prime factors.
HCF = 22 x 3 x 7
= 4 X 3 X 7
= 84

EVALUATION
Find the HCF of the number 36, 54 and 60
Further Studies
Read More...
Read More...
https://youtu.be/rAnhIZPDzlY
LESSON 15
SQUARE ROOTS OF PERFECT SQUARES BY FACTOR METHOD
SQUARE:
72 = 7 X 7
In words ‘the square of 7 is 49’. We can turn this statement round and say, ‘the square root of 49 is 7’.
In symbols, √49 = 7, to find the square root of a number, first find its factors.
Example 1
Find √(11025.)
Method: try the prime number, first find its factors.
3 11025
3 3675
5 1225
5 245
7 49
7 7
1
11025 = 32 X 52 X 72
= (3X5X7) X (3 X 5 X 7)
= 105 X 105
Thus √11025 = 105

It is not always necessary to write a number in its prime factors.
Perfect Squares:
A perfect square is a whole number whose square root is also is also a whole number. i.e. 9, 25, 225,9216 are perfect squares because their square roots are whole numbers.
It is possible to express a perfect square in factors with even indices. For example:
9216 = 962 = 32 X 322
= 32 X 42 X 82
= 32 X 210
Example 2: Find the smallest number by which 540 must be multiplied so that the product is a perfect square.
2 540
2 270
3 135
3 45
3 15
5 5
1
540 = 22 X 33 X 5
The index of 2 is even.
The indices of 3 and 5 are odd.
one more 3 and one more 5 will make all the indices even. The product will then be a perfect square.
∴ The number required = 3 X 5 = 15.
Evaluation
Find by factors the square roots of the following: i. 484 ii. 2500
Find the smallest numbers by which the following must be multiplied so that their products are perfect squares. (a) 2 X 2 X 2 X 3 X 3 X 5 (b) 23 X 34 X 56 X 72 X 132

LESSON 16
Quantitative Reasoning Problems on Whole Number, LCM, HCF and Square Root of Perfect Square
Sample A 4, 8, 12, 16, 20,...
2, 4, 6, 8, 10,…
6, 12, 18, 24, 30, …
Supply the missing numbers in 16, 20, _____, 28, _______
The set are multiples of 4 because 4 can divide all the given numbers without remainder,
so successive addition of 4 gives 16 + 4 = 20, 20+ 4 = 24; 24 + 4 = 28; 28+ 4 = 32
Fill in the gaps.
15, 30, _____, 60, ___
4, 6, __, __, 12, 14
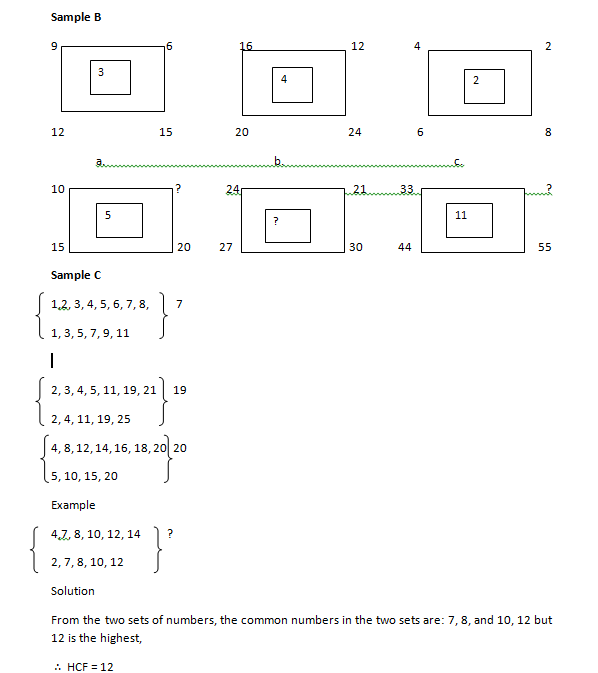
From the two sets of numbers, the common numbers in the two sets are: 7, 8, and 10, 12 but 12 is the highest,
∴ HCF = 12
Further Studies
Read More...
Read More...
https://youtu.be/rjSCMUOuy_Y
Assignment
New General Mathematics for Jss2 UBE Edition pg 13 – 22
Attempt Ex. 2d 1-5; 1e 1-5 & 1f 1
TOPIC: LCM, HCF & Square Root of Perfect Squares by Factors
CONTENT:
The least Common Multiples (LCM) of numbers
The Highest Common Factor (HCF) of numbers.
Square roots of perfect squares by factor method.
quantitative reasoning problems on whole number, LCM, HCF and Square root of perfect square
The least Common Multiples (LCM) of numbers
The LCM of two or more quantities is the smallest common multiple they have.
For example:
The multiple of 2: 2, 4, 6, 8, 10, 12…
The multiple of 3: 3, 6, 9, 12, 15…
Notice that 6 and 12 are the common multiples of 2 & 3
But the Least Common multiple (LCM) is 6.
Example 1
Find the LCM of 22, 30 and 40
Method: express each number as a product of its prime factors.
22 = 2 x 11
30 = 2 x 3 x 5
40 = 2 x 2 x 2 x5 = 23 x 5
The prime factors of 22, 30 and 40 are 2, 3, 5, and 11.
The highest power of each prime factor must be in the LCM.
These are 23, 3, 5 and 11
Thus, LCM = 23 X 3 X 5 X 11
= 8 X 3 X 5 X 11
= 1320
Alternative method
2 22 30 40
2 11 15 20
2 11 15 10
3 11 15 5
5 11 5 5
11 11 1 1
1 1 1
Thus, LCM = 23 X 3 X 5 X 11 = 1320

EVALUATION
Find the LCM of the following:
18, 30 and 48
8, 10 and 12
Further Studies
Read More...
LESSON 14
The Highest Common Factor (HCF) of numbers
14 is the highest common factor (HCF) of 28 and 42. It is the greatest number which will divide exactly into both 28 and 42.
Example 1
Find the HCF of 504 and 588.
Method: express each number as a product of its prime factors.
2 504 2 588
2 252 2 294
2 126 3 147
3 63 7 49
3 21 7 7
7 7 1
1
504 = 23 x 32 x 7 588 = 22 x 3 x 72
Find the common prime factors
504 = (22 x 3 x 7) x 2 x 3
588 = (22 x 3 x 7) x 7
The HCF is the product of the common prime factors.
HCF = 22 x 3 x 7
= 4 X 3 X 7
= 84

EVALUATION
Find the HCF of the number 36, 54 and 60
Further Studies
Read More...
Read More...
https://youtu.be/rAnhIZPDzlY
LESSON 15
SQUARE ROOTS OF PERFECT SQUARES BY FACTOR METHOD
SQUARE:
72 = 7 X 7
In words ‘the square of 7 is 49’. We can turn this statement round and say, ‘the square root of 49 is 7’.
In symbols, √49 = 7, to find the square root of a number, first find its factors.
Example 1
Find √(11025.)
Method: try the prime number, first find its factors.
3 11025
3 3675
5 1225
5 245
7 49
7 7
1
11025 = 32 X 52 X 72
= (3X5X7) X (3 X 5 X 7)
= 105 X 105
Thus √11025 = 105

It is not always necessary to write a number in its prime factors.
Perfect Squares:
A perfect square is a whole number whose square root is also is also a whole number. i.e. 9, 25, 225,9216 are perfect squares because their square roots are whole numbers.
It is possible to express a perfect square in factors with even indices. For example:
9216 = 962 = 32 X 322
= 32 X 42 X 82
= 32 X 210
Example 2: Find the smallest number by which 540 must be multiplied so that the product is a perfect square.
2 540
2 270
3 135
3 45
3 15
5 5
1
540 = 22 X 33 X 5
The index of 2 is even.
The indices of 3 and 5 are odd.
one more 3 and one more 5 will make all the indices even. The product will then be a perfect square.
∴ The number required = 3 X 5 = 15.
Evaluation
Find by factors the square roots of the following: i. 484 ii. 2500
Find the smallest numbers by which the following must be multiplied so that their products are perfect squares. (a) 2 X 2 X 2 X 3 X 3 X 5 (b) 23 X 34 X 56 X 72 X 132

LESSON 16
Quantitative Reasoning Problems on Whole Number, LCM, HCF and Square Root of Perfect Square
Sample A 4, 8, 12, 16, 20,...
2, 4, 6, 8, 10,…
6, 12, 18, 24, 30, …
Supply the missing numbers in 16, 20, _____, 28, _______
The set are multiples of 4 because 4 can divide all the given numbers without remainder,
so successive addition of 4 gives 16 + 4 = 20, 20+ 4 = 24; 24 + 4 = 28; 28+ 4 = 32
Fill in the gaps.
15, 30, _____, 60, ___
4, 6, __, __, 12, 14

From the two sets of numbers, the common numbers in the two sets are: 7, 8, and 10, 12 but 12 is the highest,
∴ HCF = 12
Further Studies
Read More...
Read More...
https://youtu.be/rjSCMUOuy_Y
Assignment
New General Mathematics for Jss2 UBE Edition pg 13 – 22
Attempt Ex. 2d 1-5; 1e 1-5 & 1f 1
WEEK 5
LESSON 17
TOPIC: Fractions
CONTENT:
Conversion of simple fractions to ratios
Conversion of simple fractions to decimals
Conversion of simple fractions to percentages
Quantitative reasoning on ratios, decimals and percentages.
Conversion of Fractions to Ratios
Ratio is a type of measure of the relative size of two or more quantities expressed as a proportion. It is used to compare the sizes of two or more quantities. For example, if in a class of 35 students, 14 are girls, then the ratio of girls to boys is 14 to 21 written as 14:21 or the ratio of boys to girls is 21 to 14 (21:14). This ratio means that for every 14 girls there are 21 boys. This can be simplified by dividing each part by 7. Then for every 2 girls there are 3 boys. That is 14:21 is equivalent to 2:3. The ratio 2:3 is the simplest form of 14:21.
Ratio can be written in any of the following three ways:
14 to 21 or 2:3
14:21 or 2:3
14/21 or 2/3
14/21 or 2/3, Shows that all ratios may be looked at as fractions and therefore, be multiplied or divide by the same number without altering its value.
NOTE: Ratio involving quantities (units) must be the same in units.
https://youtu.be/RQ2nYUBVvqI
Examples:
If Honesty spent N224.00 on buying a story book , Sandra spent N70.00 Bobo drink,
Then (amount spent Honesty)/(amount spent by Sandra)=224/70=32/10.
∴ the ratio of amount spent by Honesty to the amount spent by Sandra = 224:70 = 32:10. Reducing it to its lowest term = 16:5.
Express 49.00 as a fraction and as ratio of 84.00
Solutions
As a fraction: N49/N84=7/12
As a ratio: N49: N84 = 7:12
Express 1kg as a ratio of 150g.
Solutions:
1kg:150g = 1000g:150g = 100:15 = 20:3
In a school of 720 students the ratio of boys to girls is 7:5. Find the number of boys and girls respectively.
Solution:
Ratio of boys to girls = 7:5
Total ratio = 7+5 = 12
Number of boys = 7/12 of 720 = 7/12 x 720/1 = 7 x 60 = 420 boys
Number of girls = = 5/12 x = 720/1 = 5 x 60 = 300girls

Evaluation:
120,000 dollars is shared between 2 students who are on scholarship in Deeper Life High School in the ratio 36:28. How much does each student gets?
If the ratio of a number to 4 is equal to the ratio 3:2, find the number.
https://youtu.be/H9_3ChJ8yzM
LESSON 18
CONVERSION OF FRACTIONS TO DECIMALS.
There are two methods of doing this conversion. There is the general method which can be used any time and on any type of vulgar fraction. There is also another method where the denominator of the fraction contains power/powers of ten.
In this second case, the given fraction can first be converted to an equivalent fraction.
Examples :
Convert the following common fractions to decimal fractions (decimal numbers).
2/5 , 3/4 , 144/225 .
Solutions:
First: we can use the equivalent fractions method, before the general method.
Write 2/5 as 2/5 = (2 × 2)/(5 × 2) = 4/10 = 0.4 2/5 = 0.4
Write 3/4 as 3/4 = (3 × 25)/(4 × 25) = 75/100 = 0.75 ∴3/4 = 0.75
Write 144/225 as 144/225 = (144 × 4)/(225 × 4) = 576/1000 = 0.576 ∴ 144/225 = 0.576

Second: the general method (for all condition) is used when the denominator of the given fraction does not contain power(s) of 10. This is by dividing the numerator by the denominator mentally or via long-division previously learnt by students in their Primary School days.
Conversion of decimals to fractions.
Examples:
Convert 0.65 to a common fraction.
Solution:
To do this we simply multiply the given decimal fraction by 100 and at the same time divide it by 100.
Write 0.65 as 0.65 = (0.65 × 100)/100 . If we carefully notice the expression we will see that what we are doing is just multiplying 0.65 by unity
(1). Because 100/100= 1.
⇒(0.65 × 100)/100 = 65/100 = 13/20 , (when further reduced to the lowest term). ∴ 0.65 =13/20 .
Convert 0.6 to a common fraction.
Solution:
To do this we simply multiply the given decimal fraction by 10 and at the same time divide it by 10.
Write 0.6 as 0.6 = (0.6 × 10)/10 = 6/10 = 3/5 . ⇒ ∴ 0.6 =3/5 .
Convert 0.125 to a common fraction.
Solution:
To do this we multiply the given decimal fraction by 1000 and at the same time divide it by 1000 to have 0.125 = (0.125 × 1000)/1000 = 125/1000 = 25/200 = 5/40 = 1/8 , ( when fully simplified to its lowest form ).

EVALUATION:
Change the following common fractions to decimal fractions.
9/15 , 1/19 , 2/23 , 17/3 , 123/341 .
2. Change the following decimal fractions to the vulgar or common fractions.
0.56 , 0.0015 , 5.35 , 0.222 , 1.98

https://youtu.be/do_IbHId2Os
LESSON 19
CONVERSION OF FRACTIONS TO PERCENTAGES.
Examples :
Express 2/15as percentage.
Solution:
There are two possible ways to answer the question.
METHOD 1:
Write 2/15as 2/15×100 = 200/15 =13 1/3%.
2/15 = 13 1/3%in percentage.
METHOD 2:
Write 2/15 as (2⁄3)/(15⁄3) = (2⁄3)/5 = (2/3 ×20)/(5×20) = (40⁄3)/100 = (13 1/3)/100 = 13 1/3%in percentage.

Conversion of percentages to fractions.
Examples:
Express 65% as fraction.
Solution:
Write 65% as 65% = 65/100 = 13/20 . 65% =13/20 .
Express 24% as fraction .
Solution:
Write 24% as 24% = 24/100 =6/25 . ∴24% =6/25 .
Express 0.35% as fraction.
Solution:
Write 0.35% as 0.35% = (0.35)/100 = (0.35 × 100)/(100 × 100) = 35/10000 =7/2000 .
https://youtu.be/kmVfZ9o-2gg
EVALUATION:
Express each of the following fractions as percentage.
5/8 , 17/20 , 9/25 , 1/90 .
Express each of the following percentages as fraction.
64% , 45 % , 0.125 % , 0.17 % .

Further Studies
Read More...
https://youtu.be/CT6IqIb7urs
QUANTITATIVE REASONING (RATIOS, DECIMALS & PERCENTAGES).

https://youtu.be/USmit5zUGas
https://youtu.be/-U5N5Y5pWc8
ASSIGNMENT:
Textbook: NEW GENERAL MATHEMATICS for Junior Secondary Schools 2 (UBE Edition) page 78 to 85
Textbook: NEW GENERAL MATHEMATICS for Junior Secondary Schools 2 (UBE Edition): page 78, Ex. 9a: Q1 to Q6; page 80, Ex. 9c: Q1 to Q12; page 81, Ex.9c: Q1 to Q20
TOPIC: Fractions
CONTENT:
Conversion of simple fractions to ratios
Conversion of simple fractions to decimals
Conversion of simple fractions to percentages
Quantitative reasoning on ratios, decimals and percentages.
Conversion of Fractions to Ratios
Ratio is a type of measure of the relative size of two or more quantities expressed as a proportion. It is used to compare the sizes of two or more quantities. For example, if in a class of 35 students, 14 are girls, then the ratio of girls to boys is 14 to 21 written as 14:21 or the ratio of boys to girls is 21 to 14 (21:14). This ratio means that for every 14 girls there are 21 boys. This can be simplified by dividing each part by 7. Then for every 2 girls there are 3 boys. That is 14:21 is equivalent to 2:3. The ratio 2:3 is the simplest form of 14:21.
Ratio can be written in any of the following three ways:
14 to 21 or 2:3
14:21 or 2:3
14/21 or 2/3
14/21 or 2/3, Shows that all ratios may be looked at as fractions and therefore, be multiplied or divide by the same number without altering its value.
NOTE: Ratio involving quantities (units) must be the same in units.
https://youtu.be/RQ2nYUBVvqI
Examples:
If Honesty spent N224.00 on buying a story book , Sandra spent N70.00 Bobo drink,
Then (amount spent Honesty)/(amount spent by Sandra)=224/70=32/10.
∴ the ratio of amount spent by Honesty to the amount spent by Sandra = 224:70 = 32:10. Reducing it to its lowest term = 16:5.
Express 49.00 as a fraction and as ratio of 84.00
Solutions
As a fraction: N49/N84=7/12
As a ratio: N49: N84 = 7:12
Express 1kg as a ratio of 150g.
Solutions:
1kg:150g = 1000g:150g = 100:15 = 20:3
In a school of 720 students the ratio of boys to girls is 7:5. Find the number of boys and girls respectively.
Solution:
Ratio of boys to girls = 7:5
Total ratio = 7+5 = 12
Number of boys = 7/12 of 720 = 7/12 x 720/1 = 7 x 60 = 420 boys
Number of girls = = 5/12 x = 720/1 = 5 x 60 = 300girls

Evaluation:
120,000 dollars is shared between 2 students who are on scholarship in Deeper Life High School in the ratio 36:28. How much does each student gets?
If the ratio of a number to 4 is equal to the ratio 3:2, find the number.
https://youtu.be/H9_3ChJ8yzM
LESSON 18
CONVERSION OF FRACTIONS TO DECIMALS.
There are two methods of doing this conversion. There is the general method which can be used any time and on any type of vulgar fraction. There is also another method where the denominator of the fraction contains power/powers of ten.
In this second case, the given fraction can first be converted to an equivalent fraction.
Examples :
Convert the following common fractions to decimal fractions (decimal numbers).
2/5 , 3/4 , 144/225 .
Solutions:
First: we can use the equivalent fractions method, before the general method.
Write 2/5 as 2/5 = (2 × 2)/(5 × 2) = 4/10 = 0.4 2/5 = 0.4
Write 3/4 as 3/4 = (3 × 25)/(4 × 25) = 75/100 = 0.75 ∴3/4 = 0.75
Write 144/225 as 144/225 = (144 × 4)/(225 × 4) = 576/1000 = 0.576 ∴ 144/225 = 0.576

Second: the general method (for all condition) is used when the denominator of the given fraction does not contain power(s) of 10. This is by dividing the numerator by the denominator mentally or via long-division previously learnt by students in their Primary School days.
Conversion of decimals to fractions.
Examples:
Convert 0.65 to a common fraction.
Solution:
To do this we simply multiply the given decimal fraction by 100 and at the same time divide it by 100.
Write 0.65 as 0.65 = (0.65 × 100)/100 . If we carefully notice the expression we will see that what we are doing is just multiplying 0.65 by unity
(1). Because 100/100= 1.
⇒(0.65 × 100)/100 = 65/100 = 13/20 , (when further reduced to the lowest term). ∴ 0.65 =13/20 .
Convert 0.6 to a common fraction.
Solution:
To do this we simply multiply the given decimal fraction by 10 and at the same time divide it by 10.
Write 0.6 as 0.6 = (0.6 × 10)/10 = 6/10 = 3/5 . ⇒ ∴ 0.6 =3/5 .
Convert 0.125 to a common fraction.
Solution:
To do this we multiply the given decimal fraction by 1000 and at the same time divide it by 1000 to have 0.125 = (0.125 × 1000)/1000 = 125/1000 = 25/200 = 5/40 = 1/8 , ( when fully simplified to its lowest form ).

EVALUATION:
Change the following common fractions to decimal fractions.
9/15 , 1/19 , 2/23 , 17/3 , 123/341 .
2. Change the following decimal fractions to the vulgar or common fractions.
0.56 , 0.0015 , 5.35 , 0.222 , 1.98

https://youtu.be/do_IbHId2Os
LESSON 19
CONVERSION OF FRACTIONS TO PERCENTAGES.
Examples :
Express 2/15as percentage.
Solution:
There are two possible ways to answer the question.
METHOD 1:
Write 2/15as 2/15×100 = 200/15 =13 1/3%.
2/15 = 13 1/3%in percentage.
METHOD 2:
Write 2/15 as (2⁄3)/(15⁄3) = (2⁄3)/5 = (2/3 ×20)/(5×20) = (40⁄3)/100 = (13 1/3)/100 = 13 1/3%in percentage.

Conversion of percentages to fractions.
Examples:
Express 65% as fraction.
Solution:
Write 65% as 65% = 65/100 = 13/20 . 65% =13/20 .
Express 24% as fraction .
Solution:
Write 24% as 24% = 24/100 =6/25 . ∴24% =6/25 .
Express 0.35% as fraction.
Solution:
Write 0.35% as 0.35% = (0.35)/100 = (0.35 × 100)/(100 × 100) = 35/10000 =7/2000 .
https://youtu.be/kmVfZ9o-2gg
EVALUATION:
Express each of the following fractions as percentage.
5/8 , 17/20 , 9/25 , 1/90 .
Express each of the following percentages as fraction.
64% , 45 % , 0.125 % , 0.17 % .

Further Studies
Read More...
https://youtu.be/CT6IqIb7urs
QUANTITATIVE REASONING (RATIOS, DECIMALS & PERCENTAGES).

https://youtu.be/USmit5zUGas
https://youtu.be/-U5N5Y5pWc8
ASSIGNMENT:
Textbook: NEW GENERAL MATHEMATICS for Junior Secondary Schools 2 (UBE Edition) page 78 to 85
Textbook: NEW GENERAL MATHEMATICS for Junior Secondary Schools 2 (UBE Edition): page 78, Ex. 9a: Q1 to Q6; page 80, Ex. 9c: Q1 to Q12; page 81, Ex.9c: Q1 to Q20
WEEK 6
LESSON 20
Topic: Conversion of fractions to decimal
Specific topic: Changing fractions to decimal
Reference book: Maths Inside out, Page 100
Behavioral objective: At the end of the lesson, student should be able to: change fraction to decimals.

View Content 1 below

further studies
Read More...
practice test
Read More...
http://www.youtube.com/watch?v=Gn2pdkvdbGQ
LESSON 21
Topic: Changing Decimal to Fraction
Reference book: Maths Inside out, Page 99
Behavioral objective: At the end of the lesson, student should be able to: change given decimal numbers to fractions.

View Content 2 below

further studies
Read More...
Read More...
practice test
Short Practice Test
https://www.youtube.com/watch?v=Mst8iZjIpFE
LESSON 22
Topic: Ordering of decimals
Reference book: Maths Inside out, Page 101
Behavioral objective: At the end of the lesson, student should be able to: arrange decimals in ascending or descending order of Magnitude

View Content 3 below

further studies
Read More...
Read More...
Read More...
http://www.youtube.com/watch?v=wH3YWhViBtw
play game
Maths Game
Maths Game
LESSON 23
Topic: Metric weight in Decimal Fraction
Reference book: Maths Inside out, Page 100
Behavioral objective: At the end of the lesson, student should be able to: write given metric weight in decimals form
View Content 4 below

further studies
Read More...
https://www.youtube.com/watch?v=3R10voA9BEo
LESSON 24
Topic: Conversion of fractions to decimal and vice versa
Behavioral objective: At the end of the lesson, student should be able to: (i) express fractions as decimals (ii) arrange decimals in order of magnitude (iii) change decimals to fraction. (iv) write metric weight in decimal.
Reference book: Maths Inside out, Page 98
View Content 5 below

further studies
Read More...
Read More...
Read More...
practice test
Short Practice Test
LESSON 25
Topic: Inequalities and linear Equations
Specific topic: Solving linear equations
Behavioral objective: At the end of the lesson, student should be able to: solve given linear equations
Reference book: New General Maths for JSS 3 Page 207
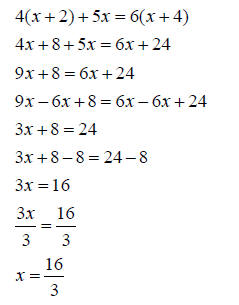
View Content 6 below


practice test
Short Practice Test
Short Practice Test
watch video
http://www.youtube.com/watch?v=ldYGiXSHa_Q
LESSON 26
Topic: Solving inequalities
Behavioral objective: At the end of the lesson, student should be able to: solve for the unknown variables in given inequalities
Reference book: New General Maths for JSS 3 Page 208

View Content 7 below

Solving an Inequality
An inequality is similar to an equation. There are two expressions separated by a symbol that indicates how one expression is related to the other. In an equation such as 7x = 49, the = sign indicates that the expressions are equivalent. In an inequality, such as 7x > 49, the > sign indicates that the left side is larger than the right side.
To solve the inequality 7x > 49, we follow the same rules that we did for equations. In this case, divide both sides by 7 so that x > 7. This means that x is a value and it is always larger than 7, and never equal to or less than 7.
The "less than" symbol (<) may also be seen in inequalities.
further studies
Read More...
practice test
Short Practice Test
http://www.youtube.com/watch?v=5G7GWe2DrKc
LESSON 27
Topic: Simplifying linear equation
Behavioral objective: At the end of the lesson, student should be able to: simplify given linear equation
Reference book: New General Maths for JSS 3 Page 209

View Content 8 below

further studies
Read More...
watch video
http://www.youtube.com/watch?v=tdiNDwKOBvw
LESSON 28
Topic: Expanding linear Equation
Behavioral objective: At the end of the lesson, student should be able to: expand given linear equation
Reference book: New General Maths for JSS 3 Page 209
View Content 9 below

https://www.youtube.com/watch?v=P80FKNYBe24
https://www.youtube.com/watch?v=6SzLLRDnJYE
LESSON 29
Topic: factorizing equation
Behavioral objective: At the end of the lesson, student should be able to: factorize given algebraic equations
Reference book: New General Maths for JSS 3 Page 209
View Content 10 below

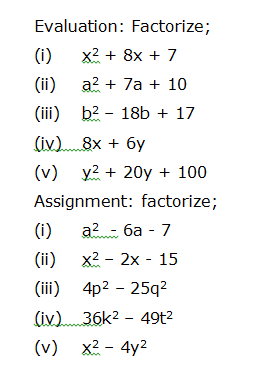
further studies
Read More...
factor any expression in algebra
more...
https://www.youtube.com/watch?v=tm49BYGw_Sg
Topic: Conversion of fractions to decimal
Specific topic: Changing fractions to decimal
Reference book: Maths Inside out, Page 100
Behavioral objective: At the end of the lesson, student should be able to: change fraction to decimals.

View Content 1 below

further studies
Read More...
practice test
Read More...
http://www.youtube.com/watch?v=Gn2pdkvdbGQ
LESSON 21
Topic: Changing Decimal to Fraction
Reference book: Maths Inside out, Page 99
Behavioral objective: At the end of the lesson, student should be able to: change given decimal numbers to fractions.

View Content 2 below

further studies
Read More...
Read More...
practice test
Short Practice Test
https://www.youtube.com/watch?v=Mst8iZjIpFE
LESSON 22
Topic: Ordering of decimals
Reference book: Maths Inside out, Page 101
Behavioral objective: At the end of the lesson, student should be able to: arrange decimals in ascending or descending order of Magnitude

View Content 3 below

further studies
Read More...
Read More...
Read More...
http://www.youtube.com/watch?v=wH3YWhViBtw
play game
Maths Game
Maths Game
LESSON 23
Topic: Metric weight in Decimal Fraction
Reference book: Maths Inside out, Page 100
Behavioral objective: At the end of the lesson, student should be able to: write given metric weight in decimals form

View Content 4 below

further studies
Read More...
https://www.youtube.com/watch?v=3R10voA9BEo
LESSON 24
Topic: Conversion of fractions to decimal and vice versa
Behavioral objective: At the end of the lesson, student should be able to: (i) express fractions as decimals (ii) arrange decimals in order of magnitude (iii) change decimals to fraction. (iv) write metric weight in decimal.
Reference book: Maths Inside out, Page 98

View Content 5 below


further studies
Read More...
Read More...
Read More...
practice test
Short Practice Test
LESSON 25
Topic: Inequalities and linear Equations
Specific topic: Solving linear equations
Behavioral objective: At the end of the lesson, student should be able to: solve given linear equations
Reference book: New General Maths for JSS 3 Page 207
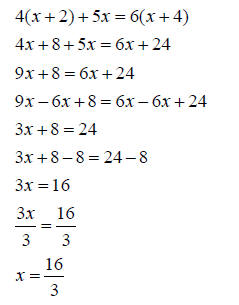
View Content 6 below


practice test
Short Practice Test
Short Practice Test
watch video
http://www.youtube.com/watch?v=ldYGiXSHa_Q
LESSON 26
Topic: Solving inequalities
Behavioral objective: At the end of the lesson, student should be able to: solve for the unknown variables in given inequalities
Reference book: New General Maths for JSS 3 Page 208

View Content 7 below

Solving an Inequality
An inequality is similar to an equation. There are two expressions separated by a symbol that indicates how one expression is related to the other. In an equation such as 7x = 49, the = sign indicates that the expressions are equivalent. In an inequality, such as 7x > 49, the > sign indicates that the left side is larger than the right side.
To solve the inequality 7x > 49, we follow the same rules that we did for equations. In this case, divide both sides by 7 so that x > 7. This means that x is a value and it is always larger than 7, and never equal to or less than 7.
The "less than" symbol (<) may also be seen in inequalities.
further studies
Read More...
practice test
Short Practice Test
http://www.youtube.com/watch?v=5G7GWe2DrKc
LESSON 27
Topic: Simplifying linear equation
Behavioral objective: At the end of the lesson, student should be able to: simplify given linear equation
Reference book: New General Maths for JSS 3 Page 209

View Content 8 below

further studies
Read More...
watch video
http://www.youtube.com/watch?v=tdiNDwKOBvw
LESSON 28
Topic: Expanding linear Equation
Behavioral objective: At the end of the lesson, student should be able to: expand given linear equation
Reference book: New General Maths for JSS 3 Page 209
View Content 9 below

https://www.youtube.com/watch?v=P80FKNYBe24
https://www.youtube.com/watch?v=6SzLLRDnJYE
LESSON 29
Topic: factorizing equation
Behavioral objective: At the end of the lesson, student should be able to: factorize given algebraic equations
Reference book: New General Maths for JSS 3 Page 209
View Content 10 below

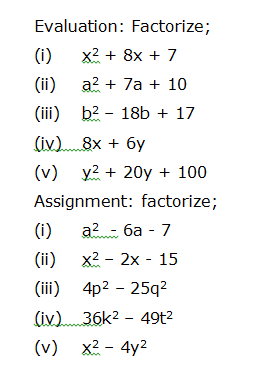
further studies
Read More...
factor any expression in algebra
more...
https://www.youtube.com/watch?v=tm49BYGw_Sg
WEEK 7
LESSON 30
TOPIC: TRANSACTIONS IN THE HOMES AND OFFICES
CONTENT:
Household Arithmetic
Commercial Arithmetic (profit & lost, interest, discount and commission)
Value orientation
Household Arithmetic
Discount buying
A discount is a reduction in price. Discounts are often given for paying in cash.
Example 1:
A trader sells packets of tissues at N140 each or four for N440. How much is saved by buying four packets at once instead of separately?
Solution
I packet of tissues = N140
4 packets = 4 X N140 = N560
Discount price of 4 packets = N440
Saving = N560 - N440 = N120
Example 2:
A radio costs N5400. A 12 ½ % discount is given for cash. What is the cash price?
Solution
Method 1:
Discount = 12 ½ % of N5400
= 12 ½ /100 of N5400
=25/2×1/100 ofN5400
= 1/8×N5400=N675
cash price = N5400-N675
= N4725
Method 2:
cash price=(100%-12 1/2%)of N5400
= 87 1/2% of N5400
= (87 1/2)/100 × N5400=7/8×N5400
= N4725

Evaluation
The selling price of a chair is N14000. The trader gives a 25% discount for cash. What is the cash price?
Find the discount price if a discount price of:
10% is given on a cost price of N430
12 ½ % is given on a cost price of N280
https://youtu.be/GCmzEzIufRU
LESSON 31
Instalment buying
An instalment is a part payment. Many people find it easier to buy expensive items by paying instalments.
Buying by instalment is called hire purchase. The buyer hires the use of an item before paying for it completely. This is why hire purchase is more costly than paying in cash.
Example
The cost of a DVD player is either N34000 in cash or deposit of N4000, and 12 monthly payments of N2750. Find the difference between the instalment price and the cash price.
Solution
Instalment price = deposit + instalment
= N4000 + 12 X N2750
= N4000 + N33000
= N37000
Price difference = - N34000
= N3000
Evaluation
The hire purchase price of a computer is N84000. 25% is paid as a deposit. The rest is spread over 12 equal monthly instalments.
Calculate the amount of the deposit.
Calculate the remainder to be paid.
Find the amount of each monthly instalment.
https://youtu.be/rOp3GPnKJXI
LESSON 32
Civic arithmetic
Value Added Tax (VAT)
A proportion of the money paid for certain goods and services is given to the Government. The part which is given to the Government is called Value Added Tax (VAT), the goods and services are called VATable items.
https://www.youtube.com/watch?v=6ajIe-5fC4M
Example 1
An advertisement for a table says that its price is N15,300 plus 5% VAT. how much does the customer pay?
Amount paid by customer = 105% of N15300
= N15300 X 105/100
= N16065
Note: The difference between N16065 and N15300 is N765. The Government receives N765 as Vat
Example 2
One year a company paid a N94500 telephone bill to NITEL. The bill included VAT at 5%. Calculate how much money the Government receives as VAT on the bill.
Solution
Since N94500 includes 5% VAT, then N94500 is 105% of the actual telephone bill. The VAT is 5% of the actual telephone bill.
1% of actual bill = N94500 /105
= N900
5% of actual bill = N900 X 5
= N 4500
The government receives N 4500 as VAT.
EVALUATION
Find the amount of money that the Government receives as VAT on each item in the following advertisement:
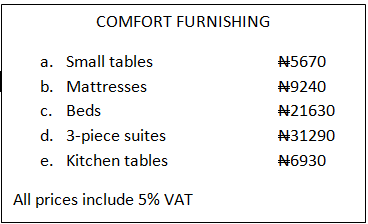
https://youtu.be/ylnynG5RGZg
LESSON 33
Bills and charges
Electricity bills – these bills are based on the number of units of electricity used. Also there is usually a standing charge, or Demand charge, VAT is charged.
Table 10.3 gives typical charges.
Cost per unit N8
Standing charge N150 per quarter
VAT 5% of total bill
Table 10.3 Typical electricity charges
Example 1
A company’s electricity meter reading changed from 45243 to 50584 in one quarter. Use Table 10.3 to calculate the company’s electricity bill.
Solution
Number of units used = 50584 – 45243
= 5341
Cost at N8 per unit = N8 X 5341
= N42728
Standing charge = N150
Total charges = N42728 + N150
= N42878
Total bill including VAT = N42878×105%
= N42878 X 105/100
= N45021.90
EVALUATION
The quarterly reading of an electricity meter by PHCN are as follows:
1st quarter----- 2nd quarter -----3rd quarter -----4th quarter
3441 -----4506 -----5798 -----5999
If the reading at the beginning of the 1st quarter was 0000.
Find the number of units of electricity consumed in each quarter.
If 1 unit cost 4K, calculate the cost of electricity consumed in each quarter.
The cost of electricity consumed throughout the four quarters.
https://youtu.be/w38H8fu170o
LESSON 34
Commercial Arithmetic
Profit & Losst
Example1:
A trader buys a kettle for and sells it at a profit of 15%. Find his actual profit and the selling price.
Solution:
Profit =15% of N800= 15/100×N800=N120
Selling price = N800 + N120 = N920
Example 2
A hat is bought for N250 and sold for N220. What is the loss per cent?
Solution
Actual loss = N250 - N220 = N30
The ratio, loss: cost = N30: N250 = 30: 250
=30/250
thus the loss is (30 )/250 of the cost price
Percentage loss = 30/250×100%=12%

EVALUATION
A farmer buys a cow for N40000 and sells it for N33000. What is the percentage loss?
A trader bought some compact disc for N350 each. She sold them at a 12% profit. What was the selling price?
https://youtu.be/NCL-kB7k30Q
LESSON 35
Simple Interest,
If you save your money with a bank, you will be paid some extra money called interest. On the other hand, if you borrow money from a bank you pay interest to the bank. The original money invested or borrowed is known as the principal or capital. The interest rate is often given in percentage and quoted as a rate per annum. For example, 5% rate means that the interest paid or received every year is 5% of the principal.
Example 1:
if you save N20000, then at the end of the year you will have your original money (principal) plus the interest
N20000 + 5% of N20000 = N20000 + N1000
= N21000
The interest is N1000 and the amount you now have in your saving account is N21000
Note that (Amount = principal + interest).
Example 2:
Mr. Ogbeha saves N50000 with a bank for 1 year with interest at 5 ½ % per annum.
Calculate the interest he will receive at the end of the year.
Calculate the simple interest for 4 ½ years.
What is the total amount he will save at the end of 4 ½ years
Solution:
Interest = 5 ½% of N50000
=5 (5 1/2)/100×N50000=(5.5)/100×N50000
= 0.055 X 50000 = N2750
Interest for 1 year = N2750
Interest for 4 ½ years = N2750 X 4 ½
= N2750 X 4.5
Simple interest = N12,375
Amount saved = principal + interest
= N50000+N12,375 = N62375

EVALUATION
Find the simple interest in question 1 to 3
10000 for 1 year at 4% per annum
15000 for 2years at 6% per annum
20000 for 1year at 4 1 ½ per annum
https://youtu.be/6AZijeJDmgY
LESSON 36
Commission
Commission is payment for selling an item. For example insurance agents get commission for selling insurance. The more insurance they sell, the more commission they get. Likewise the sales representatives often receive a proportion of the value of the goods they sell. This proportion is their commission.
Example 1
A sales representative works for an electric fan company. He gets a commission of 14k in the naira. In one week he sells four table fans at N10500 each and nine small fans at N5400 each. Calculate his commission.
Total sales = 4 X N10500 + 9 x N5400
= N42,000 + N48,600
= N90600
He gets 14k for every naira.
Commission = 90600 x 14k
= 1268400k
= N12684
Example 2
A bank charges 2 ½ % commissions for issuing a Bank Draft to its customers. If a customer obtained a Bank Draft for 84000 from the bank, calculate the total cost of the Bank Draft.
Solution
Commission paid to the bank
= 2 ½% of N84000
= 2 ½ X 1/100×N84000
= 5/200×N84000
= N2100
Total cost of Bank Draft
= value of Bank Draft + commission
= N84000 + N2100
= N86100

EVALUATION
A rent collector’s commission is 4 ½ of his takings. In one month he collects N842800 in rent. How much money does he get?
A car salesman gets 1k in the naira commission. Calculate his commission if he sells N5238000 worth of cars in a month.
https://youtu.be/olrl8uP-ZOU
Assignment
New General Mathematics for JSS 2 UBE Edition pg 87-95
Attempt Ex. 10a 1-3; 10b 2; 10c 4; 10d 2; 10e 2; 10f 2; 10g 1; 10h 3; 10i 8
TOPIC: TRANSACTIONS IN THE HOMES AND OFFICES
CONTENT:
Household Arithmetic
Commercial Arithmetic (profit & lost, interest, discount and commission)
Value orientation
Household Arithmetic
Discount buying
A discount is a reduction in price. Discounts are often given for paying in cash.
Example 1:
A trader sells packets of tissues at N140 each or four for N440. How much is saved by buying four packets at once instead of separately?
Solution
I packet of tissues = N140
4 packets = 4 X N140 = N560
Discount price of 4 packets = N440
Saving = N560 - N440 = N120
Example 2:
A radio costs N5400. A 12 ½ % discount is given for cash. What is the cash price?
Solution
Method 1:
Discount = 12 ½ % of N5400
= 12 ½ /100 of N5400
=25/2×1/100 ofN5400
= 1/8×N5400=N675
cash price = N5400-N675
= N4725
Method 2:
cash price=(100%-12 1/2%)of N5400
= 87 1/2% of N5400
= (87 1/2)/100 × N5400=7/8×N5400
= N4725

Evaluation
The selling price of a chair is N14000. The trader gives a 25% discount for cash. What is the cash price?
Find the discount price if a discount price of:
10% is given on a cost price of N430
12 ½ % is given on a cost price of N280
https://youtu.be/GCmzEzIufRU
LESSON 31
Instalment buying
An instalment is a part payment. Many people find it easier to buy expensive items by paying instalments.
Buying by instalment is called hire purchase. The buyer hires the use of an item before paying for it completely. This is why hire purchase is more costly than paying in cash.
Example
The cost of a DVD player is either N34000 in cash or deposit of N4000, and 12 monthly payments of N2750. Find the difference between the instalment price and the cash price.
Solution
Instalment price = deposit + instalment
= N4000 + 12 X N2750
= N4000 + N33000
= N37000
Price difference = - N34000
= N3000
Evaluation
The hire purchase price of a computer is N84000. 25% is paid as a deposit. The rest is spread over 12 equal monthly instalments.
Calculate the amount of the deposit.
Calculate the remainder to be paid.
Find the amount of each monthly instalment.
https://youtu.be/rOp3GPnKJXI
LESSON 32
Civic arithmetic
Value Added Tax (VAT)
A proportion of the money paid for certain goods and services is given to the Government. The part which is given to the Government is called Value Added Tax (VAT), the goods and services are called VATable items.
https://www.youtube.com/watch?v=6ajIe-5fC4M
Example 1
An advertisement for a table says that its price is N15,300 plus 5% VAT. how much does the customer pay?
Amount paid by customer = 105% of N15300
= N15300 X 105/100
= N16065
Note: The difference between N16065 and N15300 is N765. The Government receives N765 as Vat
Example 2
One year a company paid a N94500 telephone bill to NITEL. The bill included VAT at 5%. Calculate how much money the Government receives as VAT on the bill.
Solution
Since N94500 includes 5% VAT, then N94500 is 105% of the actual telephone bill. The VAT is 5% of the actual telephone bill.
1% of actual bill = N94500 /105
= N900
5% of actual bill = N900 X 5
= N 4500
The government receives N 4500 as VAT.
EVALUATION
Find the amount of money that the Government receives as VAT on each item in the following advertisement:

https://youtu.be/ylnynG5RGZg
LESSON 33
Bills and charges
Electricity bills – these bills are based on the number of units of electricity used. Also there is usually a standing charge, or Demand charge, VAT is charged.
Table 10.3 gives typical charges.
Cost per unit N8
Standing charge N150 per quarter
VAT 5% of total bill
Table 10.3 Typical electricity charges
Example 1
A company’s electricity meter reading changed from 45243 to 50584 in one quarter. Use Table 10.3 to calculate the company’s electricity bill.
Solution
Number of units used = 50584 – 45243
= 5341
Cost at N8 per unit = N8 X 5341
= N42728
Standing charge = N150
Total charges = N42728 + N150
= N42878
Total bill including VAT = N42878×105%
= N42878 X 105/100
= N45021.90
EVALUATION
The quarterly reading of an electricity meter by PHCN are as follows:
1st quarter----- 2nd quarter -----3rd quarter -----4th quarter
3441 -----4506 -----5798 -----5999
If the reading at the beginning of the 1st quarter was 0000.
Find the number of units of electricity consumed in each quarter.
If 1 unit cost 4K, calculate the cost of electricity consumed in each quarter.
The cost of electricity consumed throughout the four quarters.
https://youtu.be/w38H8fu170o
LESSON 34
Commercial Arithmetic
Profit & Losst
Example1:
A trader buys a kettle for and sells it at a profit of 15%. Find his actual profit and the selling price.
Solution:
Profit =15% of N800= 15/100×N800=N120
Selling price = N800 + N120 = N920
Example 2
A hat is bought for N250 and sold for N220. What is the loss per cent?
Solution
Actual loss = N250 - N220 = N30
The ratio, loss: cost = N30: N250 = 30: 250
=30/250
thus the loss is (30 )/250 of the cost price
Percentage loss = 30/250×100%=12%

EVALUATION
A farmer buys a cow for N40000 and sells it for N33000. What is the percentage loss?
A trader bought some compact disc for N350 each. She sold them at a 12% profit. What was the selling price?
https://youtu.be/NCL-kB7k30Q
LESSON 35
Simple Interest,
If you save your money with a bank, you will be paid some extra money called interest. On the other hand, if you borrow money from a bank you pay interest to the bank. The original money invested or borrowed is known as the principal or capital. The interest rate is often given in percentage and quoted as a rate per annum. For example, 5% rate means that the interest paid or received every year is 5% of the principal.
Example 1:
if you save N20000, then at the end of the year you will have your original money (principal) plus the interest
N20000 + 5% of N20000 = N20000 + N1000
= N21000
The interest is N1000 and the amount you now have in your saving account is N21000
Note that (Amount = principal + interest).
Example 2:
Mr. Ogbeha saves N50000 with a bank for 1 year with interest at 5 ½ % per annum.
Calculate the interest he will receive at the end of the year.
Calculate the simple interest for 4 ½ years.
What is the total amount he will save at the end of 4 ½ years
Solution:
Interest = 5 ½% of N50000
=5 (5 1/2)/100×N50000=(5.5)/100×N50000
= 0.055 X 50000 = N2750
Interest for 1 year = N2750
Interest for 4 ½ years = N2750 X 4 ½
= N2750 X 4.5
Simple interest = N12,375
Amount saved = principal + interest
= N50000+N12,375 = N62375

EVALUATION
Find the simple interest in question 1 to 3
10000 for 1 year at 4% per annum
15000 for 2years at 6% per annum
20000 for 1year at 4 1 ½ per annum
https://youtu.be/6AZijeJDmgY
LESSON 36
Commission
Commission is payment for selling an item. For example insurance agents get commission for selling insurance. The more insurance they sell, the more commission they get. Likewise the sales representatives often receive a proportion of the value of the goods they sell. This proportion is their commission.
Example 1
A sales representative works for an electric fan company. He gets a commission of 14k in the naira. In one week he sells four table fans at N10500 each and nine small fans at N5400 each. Calculate his commission.
Total sales = 4 X N10500 + 9 x N5400
= N42,000 + N48,600
= N90600
He gets 14k for every naira.
Commission = 90600 x 14k
= 1268400k
= N12684
Example 2
A bank charges 2 ½ % commissions for issuing a Bank Draft to its customers. If a customer obtained a Bank Draft for 84000 from the bank, calculate the total cost of the Bank Draft.
Solution
Commission paid to the bank
= 2 ½% of N84000
= 2 ½ X 1/100×N84000
= 5/200×N84000
= N2100
Total cost of Bank Draft
= value of Bank Draft + commission
= N84000 + N2100
= N86100

EVALUATION
A rent collector’s commission is 4 ½ of his takings. In one month he collects N842800 in rent. How much money does he get?
A car salesman gets 1k in the naira commission. Calculate his commission if he sells N5238000 worth of cars in a month.
https://youtu.be/olrl8uP-ZOU
Assignment
New General Mathematics for JSS 2 UBE Edition pg 87-95
Attempt Ex. 10a 1-3; 10b 2; 10c 4; 10d 2; 10e 2; 10f 2; 10g 1; 10h 3; 10i 8
WEEK 8
LESSON 37
TOPIC: Approximation
CONTENT:
Approximation of numbers
Quantitative reasoning on approximation
Approximation of numbers
To approximate a number means to write a number near the original number that is a number not exactly the original number. It may be a bit more or less than the original. Whole numbers can be approximated to the nearest ten, hundred, thousand, million, etc.
Let’s consider the table below:
NUMBER APPROXIMATED
186 =190 to the nearest ten
1586 =1600 to the nearest hundred
346 =300 to the nearest hundred
1481 =1480 to the nearest ten
687.4 =687 to the nearest unit
4225 =4000 to the nearest thousand
69685.42 =69690 to the nearest ten
2.634 =2.630 to the nearest thousandth
0.214 =0.214 to the nearest thousandth
From the above table, we can see that when numbers are approximated, they do not give the exact result expected. In approximation, we only consider the next figure we are approximating. If it is up to 5 and above, we take it as one (1) and add the (1) to the figure we are approximating to. If it is less than 5, we make it zero (0) and add zero to the figure.
Examples:
Sum 48, 226 and 592 and approximate your answer to the nearest hundred.
Solution:
48 + 226 +592 = 866. To the nearest hundred 866 = 900
Simply 1984 -689-800+215
Solution:
1984+215-(689+800)=2199-1489=710
To the nearest hundred = 700
The heights of three educators are 1.45m, 3m and 2.11m. Calculate the total height and approximate to the nearest hundredth.
Solution:
1.45m + 3.00m + 2.11m = 6.56m.
To the nearest hundredth 6.56m is the answer.
Note that in the example above, the answer is exactly the as the number approximated, which is 6.56m.
NOTE:
Correcting numbers to the nearest ten (10) means leaving your answer with only one zero at the back of your answer (the unit position), while to the nearest hundred (100) and thousand
(1000) means leaving two zeros and three zeros at the back respectively
Example:
Write 7822 to the (a) nearest ten (b) nearest hundred (c) thousand
Solutions:
7822 =7820 to the nearest ten because 7822 is nearer to 7820 than 7830
7822 =7800 to the nearest ten because 7822 is nearer to 7800 than 7900
7822 =8000 to the nearest ten because 7822 is nearer to 8000 than 7000
EVALUATION:
Approximate (a) 2.517 (b) 0.497 to the nearest whole, tenth and hundredth
In 2011 Nigeria general election, there were 22.8 million registered male and 25.12 million registered female voters. How voters were there altogether correct to 3 significant figures?
Quantitative Reasoning on approximation
Sample A:
237
561
798 →800
420
513
933 →930
Study the samples and then use it to answer the following:
243
115
358 →?
?
316
621 →620
512
242
? →750
Sample B:
267.167 = 267.17
107.224 = 107.22
Now solve the following:
1. 7.872 = ?
2. 100.248 = ?
3. ? = 0.89
4. ? = 0.03

https://youtu.be/fd-E18EqSVk
ASSIGNMENT:
Textbook: NEW GENERAL MATHEMATICS for JSS2 page 66 to 70
Textbook: NEW GENERAL MATHEMATICS for JSS2 Ex. 8c page 69 & Ex. 8e page 70
LESSON 38
TOPIC: Operation on Directed Numbers Charts Interpretation
CONTENT:
Addition and subtraction of directed no
Multiplication and Division of directed numbers
Tables and Charts
https://youtu.be/OAoLCXpao6s
ADDITION AND SUBTRACTION OF DIRECTED NUMBER
Numbers can be shown on a number line which extends above and below zero. This gives positive and negative numbers which is referred to as directed numbers.
The signs + and – show the directions from 0. This is illustrated below:
-5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5
Examples:
Simplify the following:
(+1) + (+3)=+4
(-3) + (+5) = +2
(+5) – (+3) = -4
(-1) – (+2) = -3
NOTE:
To add a positive number, move to the right on the number line.
To subtract a positive number, move to the left on the number line.
To add a negative number, move to the left on the number line. This is the equivalent to subtracting a positive number of the same value.
To subtract a negative number, move to the right on the number line. This is equivalent to adding a positive number of the same value.
https://youtu.be/_BgblvF90UE
MULTIPLICATION AND DIVISION OF DIRECTED NUMBERS
Positive multipliers
Multiplication is a short way of writing repeated additions. For example,
3 x 4 = 3 lots of 4
= 4 + 4 + 4
= 12
With directed numbers,
(+4) + (+4) + (+4) = 3 lots of (+4)
= 3 X (+4)
The multiplier is 3. It is positive. Thus,
(+3) X (+4) = (+4) + (+4) + (+4) = +12
(+3) X (+4)
1 X (+4)
0 +4 +12

START
The illustration above shows 1 x (+4) and (+3) x (+4) as movement on the number line. The movements are in the same direction from 0.
Similarly,
(-2)+ (-2) + (-2) + (-2) + (-2)
= 5 lots of (-2)
= 5 X (-2)
The multiplier is 5. It is positive.
Thus, (+5) x (-2)
= (-2)+ (-2) + (-2) + (-2) + (-2)
= -10
This is illustrated below:
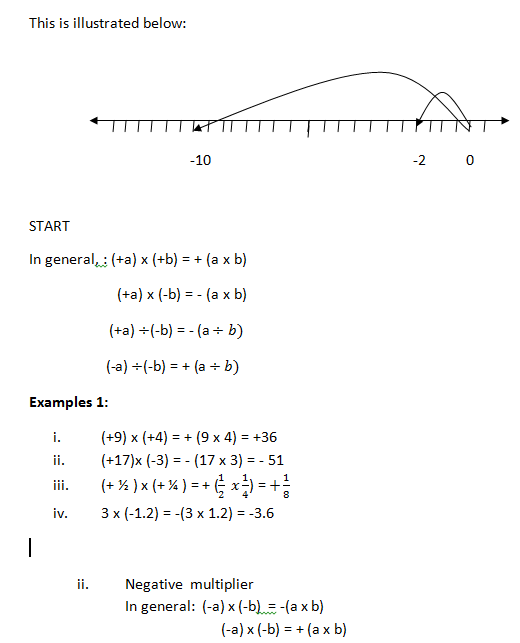
START
In general, : (+a) x (+b) = + (a x b)
(+a) x (-b) = - (a x b)
(+a) ÷(-b) = - (a ÷b)
(-a) ÷(-b) = + (a ÷b)
Examples 1:
(+9) x (+4) = + (9 x 4) = +36
(+17)x (-3) = - (17 x 3) = - 51
(+ ½ ) x (+ ¼ ) = + (1/2 x 1/4) = +1/8
3 x (-1.2) = -(3 x 1.2) = -3.6
Negative multiplier
In general: (-a) x (-b) = -(a x b)
(-a) x (-b) = + (a x b)
Examples 2
Simplify the following:
(-7) x (+4) = -(7 x 4)
(-5) x (-18)= + (5 x 18)
(-1/3) x (+2/5)= - (1/3 x 2/5)
(-4) x (-2.2) = + (4 x 2.2) = +8.8
Examples 3
simplify (–6)X(-5)/(-10)
Solution (–6)X(-5)/(-10)
=((-6)X(-5))/(-10)= (+30)/(-10)=-(30/10)=-3
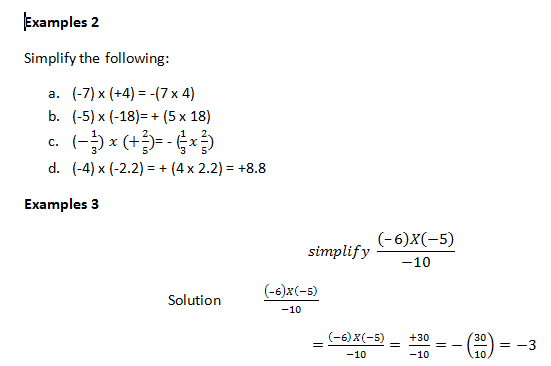
ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS 2 pg 39-44
Attempt Ex. 4e 2a-f & 4f 10a,c,e,g,h
Simplify the following:
TABLES AND CHARTS
Tables are used for arithmetic operations of numbers. It is also used to show the distance between one place and other. The set up of table differs according to its purpose.
Example
Obtain a table of addition of numbers in base 3.
Solution
+ 1 2 3
1 2 10 11
2 10 11 12
3 11 12 20

From the table above, the horizontal lines form the rows while the vertical lines form the column. The operations sign in the above example is (+). An addition of numbers in base 3, -1, +1, --- is what is illustrated in above table.
EVALUATION

https://youtu.be/K_tPbVPfHgk
TOPIC: Approximation
CONTENT:
Approximation of numbers
Quantitative reasoning on approximation

Approximation of numbers
To approximate a number means to write a number near the original number that is a number not exactly the original number. It may be a bit more or less than the original. Whole numbers can be approximated to the nearest ten, hundred, thousand, million, etc.
Let’s consider the table below:
NUMBER APPROXIMATED
186 =190 to the nearest ten
1586 =1600 to the nearest hundred
346 =300 to the nearest hundred
1481 =1480 to the nearest ten
687.4 =687 to the nearest unit
4225 =4000 to the nearest thousand
69685.42 =69690 to the nearest ten
2.634 =2.630 to the nearest thousandth
0.214 =0.214 to the nearest thousandth
From the above table, we can see that when numbers are approximated, they do not give the exact result expected. In approximation, we only consider the next figure we are approximating. If it is up to 5 and above, we take it as one (1) and add the (1) to the figure we are approximating to. If it is less than 5, we make it zero (0) and add zero to the figure.
Examples:
Sum 48, 226 and 592 and approximate your answer to the nearest hundred.
Solution:
48 + 226 +592 = 866. To the nearest hundred 866 = 900
Simply 1984 -689-800+215
Solution:
1984+215-(689+800)=2199-1489=710
To the nearest hundred = 700
The heights of three educators are 1.45m, 3m and 2.11m. Calculate the total height and approximate to the nearest hundredth.
Solution:
1.45m + 3.00m + 2.11m = 6.56m.
To the nearest hundredth 6.56m is the answer.
Note that in the example above, the answer is exactly the as the number approximated, which is 6.56m.
NOTE:
Correcting numbers to the nearest ten (10) means leaving your answer with only one zero at the back of your answer (the unit position), while to the nearest hundred (100) and thousand
(1000) means leaving two zeros and three zeros at the back respectively
Example:
Write 7822 to the (a) nearest ten (b) nearest hundred (c) thousand
Solutions:
7822 =7820 to the nearest ten because 7822 is nearer to 7820 than 7830
7822 =7800 to the nearest ten because 7822 is nearer to 7800 than 7900
7822 =8000 to the nearest ten because 7822 is nearer to 8000 than 7000
EVALUATION:
Approximate (a) 2.517 (b) 0.497 to the nearest whole, tenth and hundredth
In 2011 Nigeria general election, there were 22.8 million registered male and 25.12 million registered female voters. How voters were there altogether correct to 3 significant figures?
Quantitative Reasoning on approximation
Sample A:
237
561
798 →800
420
513
933 →930
Study the samples and then use it to answer the following:
243
115
358 →?
?
316
621 →620
512
242
? →750
Sample B:
267.167 = 267.17
107.224 = 107.22
Now solve the following:
1. 7.872 = ?
2. 100.248 = ?
3. ? = 0.89
4. ? = 0.03

https://youtu.be/fd-E18EqSVk
ASSIGNMENT:
Textbook: NEW GENERAL MATHEMATICS for JSS2 page 66 to 70
Textbook: NEW GENERAL MATHEMATICS for JSS2 Ex. 8c page 69 & Ex. 8e page 70
LESSON 38
TOPIC: Operation on Directed Numbers Charts Interpretation
CONTENT:
Addition and subtraction of directed no
Multiplication and Division of directed numbers
Tables and Charts
https://youtu.be/OAoLCXpao6s
ADDITION AND SUBTRACTION OF DIRECTED NUMBER
Numbers can be shown on a number line which extends above and below zero. This gives positive and negative numbers which is referred to as directed numbers.
The signs + and – show the directions from 0. This is illustrated below:
-5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5

Examples:
Simplify the following:
(+1) + (+3)=+4
(-3) + (+5) = +2
(+5) – (+3) = -4
(-1) – (+2) = -3
NOTE:
To add a positive number, move to the right on the number line.
To subtract a positive number, move to the left on the number line.
To add a negative number, move to the left on the number line. This is the equivalent to subtracting a positive number of the same value.
To subtract a negative number, move to the right on the number line. This is equivalent to adding a positive number of the same value.
https://youtu.be/_BgblvF90UE
MULTIPLICATION AND DIVISION OF DIRECTED NUMBERS
Positive multipliers
Multiplication is a short way of writing repeated additions. For example,
3 x 4 = 3 lots of 4
= 4 + 4 + 4
= 12
With directed numbers,
(+4) + (+4) + (+4) = 3 lots of (+4)
= 3 X (+4)
The multiplier is 3. It is positive. Thus,
(+3) X (+4) = (+4) + (+4) + (+4) = +12
(+3) X (+4)
1 X (+4)
0 +4 +12

START
The illustration above shows 1 x (+4) and (+3) x (+4) as movement on the number line. The movements are in the same direction from 0.
Similarly,
(-2)+ (-2) + (-2) + (-2) + (-2)
= 5 lots of (-2)
= 5 X (-2)
The multiplier is 5. It is positive.
Thus, (+5) x (-2)
= (-2)+ (-2) + (-2) + (-2) + (-2)
= -10
This is illustrated below:

START
In general, : (+a) x (+b) = + (a x b)
(+a) x (-b) = - (a x b)
(+a) ÷(-b) = - (a ÷b)
(-a) ÷(-b) = + (a ÷b)
Examples 1:
(+9) x (+4) = + (9 x 4) = +36
(+17)x (-3) = - (17 x 3) = - 51
(+ ½ ) x (+ ¼ ) = + (1/2 x 1/4) = +1/8
3 x (-1.2) = -(3 x 1.2) = -3.6
Negative multiplier
In general: (-a) x (-b) = -(a x b)
(-a) x (-b) = + (a x b)
Examples 2
Simplify the following:
(-7) x (+4) = -(7 x 4)
(-5) x (-18)= + (5 x 18)
(-1/3) x (+2/5)= - (1/3 x 2/5)
(-4) x (-2.2) = + (4 x 2.2) = +8.8
Examples 3
simplify (–6)X(-5)/(-10)
Solution (–6)X(-5)/(-10)
=((-6)X(-5))/(-10)= (+30)/(-10)=-(30/10)=-3
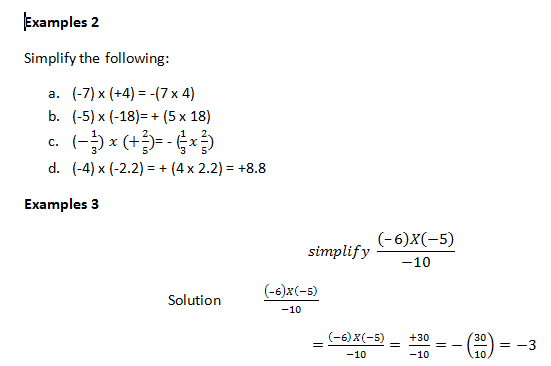
ASSIGNMENT:
NEW GENERAL MATHEMATICS JSS 2 pg 39-44
Attempt Ex. 4e 2a-f & 4f 10a,c,e,g,h
Simplify the following:
TABLES AND CHARTS
Tables are used for arithmetic operations of numbers. It is also used to show the distance between one place and other. The set up of table differs according to its purpose.
Example
Obtain a table of addition of numbers in base 3.
Solution
+ 1 2 3
1 2 10 11
2 10 11 12
3 11 12 20

From the table above, the horizontal lines form the rows while the vertical lines form the column. The operations sign in the above example is (+). An addition of numbers in base 3, -1, +1, --- is what is illustrated in above table.
EVALUATION

https://youtu.be/K_tPbVPfHgk
WEEK 9
LESSON 39
TOPIC: EXPANSION AND FACTORIZATION
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to simplify algebraic expressions containing directed numbers and terms
REFERENCE BOOK: New general maths for JSS 2 page 59
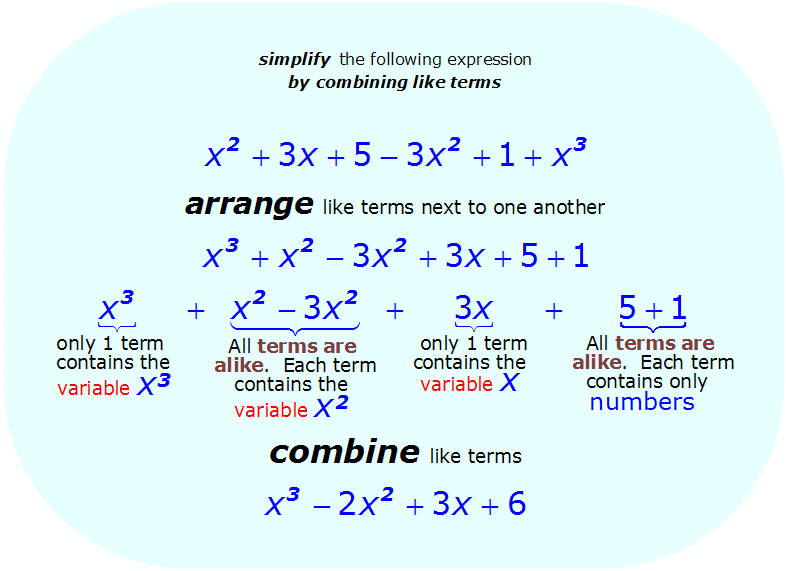
CONTENTS
Simplify
(a) -5 x 2y = -5 x (+2) x y = -10y
(b) -6 x 4x = - 6 x (-4) x x = + 24x
(c) - 3a x 7 = -3 x a x + 7 = - 3 x 7 x a = -21a
(d) - of 36 x 2 = = = -12 x 2
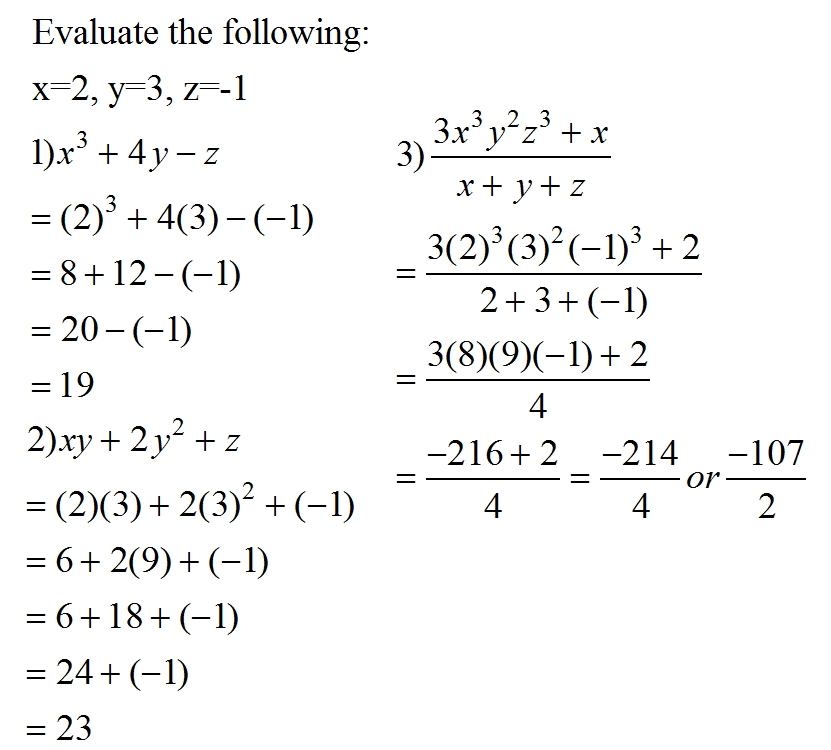
EVALUATION
Simplify the following:
a. -5 x a b. -5x x - 8 c. -3 x -2a
d. -5x x 8 e. -10 x - 3y f. 21a x - 7
g. 20y x -10 h. i.
j. 1/5 of (-45y)
further studies
Read More...
Read More...
https://www.youtube.com/watch?v=i-C_5kOmH48
LESSON 40
TOPIC: Algebraic Expressions
CONTENT:
Expansion of algebraic expressions
Factorization of simple algebraic expressions
Fractional algebraic expressions (monomial denominators)
Missing factors in algebraic expression
Quantitative Reasoning on algebraic expressions
Expansion of Algebraic Expressions
Let us evaluate the expression below: 4 x (5 + 3) or 4(5+3)
We have,
4 x (5 + 3) = 4 X 8 = 32.
Similarly,
4 x (5 +3) = 4 x 5 + 4 x 3 = 20 + 12 = 32.
Using letters (alphabets) in place of numbers,
a(b + c) or a x (b + c) = ab + ac
(b + c)a = ba + ca.
You observed that the term outside the bracket is use to multiple all the terms inside the bracket.
Examples:
Expand the following algebraic expression
4(2a+2b) 2. 3(2n + 3m – 4y)
Solutions:
4x2a + 4x2b = 8a + 8b 2. 3x2n + 3x3m -3x4y = 6n + 9m – 12y.
Now consider the expression of the form,
(a + b)(c + d).
The expansion will be: a(c + d) +b(c + d) =ac + ad +bc +bd
Examples: expand the following and simplify where necessary.
(2a – 3b) (3a – 2b) 2. (p + 2q)(3p +8q)
Solutions:
(2a – 3b) (3a – 2b) =2a(3a – 2b)– 3b(3a – 2b)
= 6a2 – 4ab – 9ab + 6b2
= 6a2 – 13ab + 6b2
. (p + 2q)(3p +8q) = p(3p +8q) + 2q(3p +8q)
=3p2 + 8pq + 6pq + 16q2
= 3p2 + 15pq + 16q2
To expand or remove brackets, use the following rules:
a(x+y)=ax+ay
a(x-y)=ax-ay
-a(x-y)=-ax+ay
-a(x+y)=-ax-ay
Note the effects negative term outside brackets in (iii) and (IV)

Evaluation:
Expand the following algebraic expression
(p-q)(r+s) 2. (3g-2)(2g-4) 3. 7(a-b) -8(a-2b) 4. (a-b)2

https://youtu.be/QXE8W-AD8pw
https://youtu.be/ffLLmV4mZwU
LESSON 41
Factorization of Simple Algebraic Expressions
A product can be expanded. That is: n(x+y)=nx+ny.
Now: n(x+y)=nx+ny.
n is a common factor of the terms nx and ny. If every term of an expression has a common factor, then the expression can be factorized.
Examples:
Factorize these expansions:
–ax-12x ii. 2xyz+5xy iii. 2abc+4ab2c iv.2abc+4ab2c
Solutions:
–ax-12x = -x(a+12)
2xyz+5xy =xy(2z+5
2abc+4ab2c =2ab(c+2b)
2abc+4ab2c =2abc(1+2b)
https://youtu.be/ctqviXu-mTE
ALGEBRAIC FRACTIONS WITH MONOMIAL DENOMINATORS
Algebraic expressions are said to have monomial denominator if the denominator has a single term. Examples are xy,4a, b2, etc. However, algebraic fraction with monomial denominators is of the form: 4/y,5/3k,2/7x,…. To effectively simplify algebraic fractions, a good knowledge of LCM is
very necessary.
Examples:
Simplify the following:
1/3a+2/3a 2. d/7c+1/21c 3. (a-2b)/3+(a-3b)/5
Solutions:
1/3a+2/3a=(1+2)/3a=3/3a=1/a
d/7c+1/21c=(3d+1)/21c=(3d+1)/21c
(a-2b)/3+(a-3b)/5=(5(a-2b)+3(a-3b))/15=(5a-10b+3a-9b)/15=(8a-19b)/15
EVALUATION:
Simplify (x+y)/2-(x+3)/3
Simplify 2/3-(x-1)/x
Factorise 6a2b – 15ab2
Simplify 6x-3y-(4x-7y)
Expand (b-a)2

https://youtu.be/M1dGE0zGoZM
MISSING FACTORS IN ALGEBRAIC EXPRESSION
Examples:
Copy and complete the following:
18ts+9t=9(……..)
3bc+9abc=3c(…….)
25t-5r=5(…….)
Solutions:
18ts+9t=9t(2s+1)
3bc+9abc=3bc(1+3a)
25t-5r=5(5t-r)
EVALUATION:
Copy and complete the following:
pqs-2qs=qs(…….)
7rs-st=(…….)
4u+2ut=(2+t)
45vt-5vr=9(…….)
9xy-6xy=(3x…….)
https://youtu.be/I-4g550Q274
QUANTITATIVE REASONING ON ALGEBRAIC EXPRESSIONS
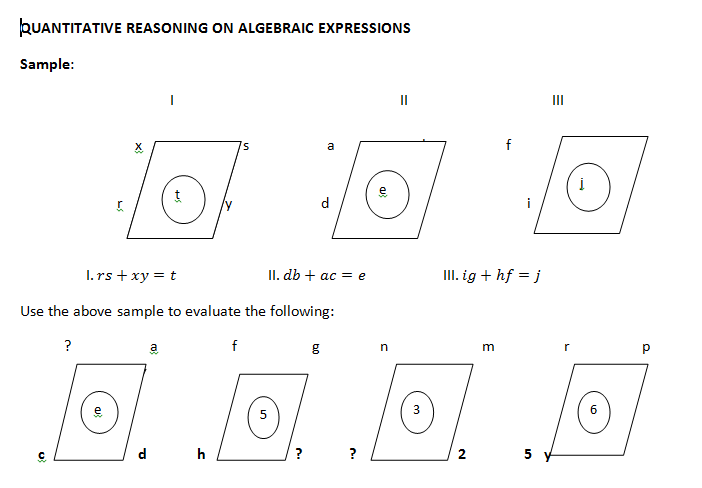
https://youtu.be/GmRixoQ5nC8
TOPIC: EXPANSION AND FACTORIZATION
PERFORMANCE OBJECTIVE: At the end of this lesson, students should be able to simplify algebraic expressions containing directed numbers and terms
REFERENCE BOOK: New general maths for JSS 2 page 59
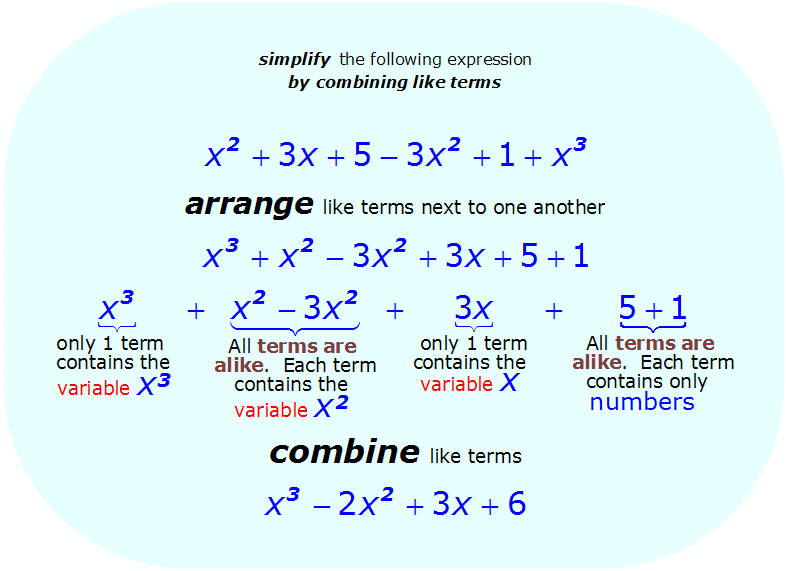
CONTENTS
Simplify
(a) -5 x 2y = -5 x (+2) x y = -10y
(b) -6 x 4x = - 6 x (-4) x x = + 24x
(c) - 3a x 7 = -3 x a x + 7 = - 3 x 7 x a = -21a
(d) - of 36 x 2 = = = -12 x 2
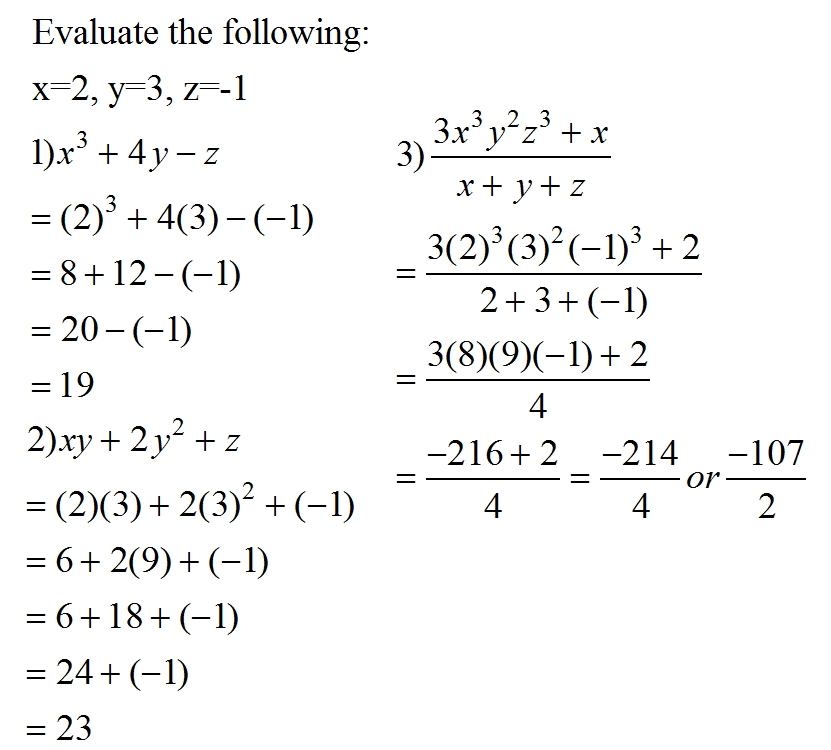
EVALUATION
Simplify the following:
a. -5 x a b. -5x x - 8 c. -3 x -2a
d. -5x x 8 e. -10 x - 3y f. 21a x - 7
g. 20y x -10 h. i.
j. 1/5 of (-45y)
further studies
Read More...
Read More...
https://www.youtube.com/watch?v=i-C_5kOmH48
LESSON 40
TOPIC: Algebraic Expressions
CONTENT:
Expansion of algebraic expressions
Factorization of simple algebraic expressions
Fractional algebraic expressions (monomial denominators)
Missing factors in algebraic expression
Quantitative Reasoning on algebraic expressions
Expansion of Algebraic Expressions
Let us evaluate the expression below: 4 x (5 + 3) or 4(5+3)
We have,
4 x (5 + 3) = 4 X 8 = 32.
Similarly,
4 x (5 +3) = 4 x 5 + 4 x 3 = 20 + 12 = 32.
Using letters (alphabets) in place of numbers,
a(b + c) or a x (b + c) = ab + ac
(b + c)a = ba + ca.
You observed that the term outside the bracket is use to multiple all the terms inside the bracket.
Examples:
Expand the following algebraic expression
4(2a+2b) 2. 3(2n + 3m – 4y)
Solutions:
4x2a + 4x2b = 8a + 8b 2. 3x2n + 3x3m -3x4y = 6n + 9m – 12y.
Now consider the expression of the form,
(a + b)(c + d).
The expansion will be: a(c + d) +b(c + d) =ac + ad +bc +bd
Examples: expand the following and simplify where necessary.
(2a – 3b) (3a – 2b) 2. (p + 2q)(3p +8q)
Solutions:
(2a – 3b) (3a – 2b) =2a(3a – 2b)– 3b(3a – 2b)
= 6a2 – 4ab – 9ab + 6b2
= 6a2 – 13ab + 6b2
. (p + 2q)(3p +8q) = p(3p +8q) + 2q(3p +8q)
=3p2 + 8pq + 6pq + 16q2
= 3p2 + 15pq + 16q2
To expand or remove brackets, use the following rules:
a(x+y)=ax+ay
a(x-y)=ax-ay
-a(x-y)=-ax+ay
-a(x+y)=-ax-ay
Note the effects negative term outside brackets in (iii) and (IV)

Evaluation:
Expand the following algebraic expression
(p-q)(r+s) 2. (3g-2)(2g-4) 3. 7(a-b) -8(a-2b) 4. (a-b)2

https://youtu.be/QXE8W-AD8pw
https://youtu.be/ffLLmV4mZwU
LESSON 41
Factorization of Simple Algebraic Expressions
A product can be expanded. That is: n(x+y)=nx+ny.
Now: n(x+y)=nx+ny.
n is a common factor of the terms nx and ny. If every term of an expression has a common factor, then the expression can be factorized.
Examples:
Factorize these expansions:
–ax-12x ii. 2xyz+5xy iii. 2abc+4ab2c iv.2abc+4ab2c
Solutions:
–ax-12x = -x(a+12)
2xyz+5xy =xy(2z+5
2abc+4ab2c =2ab(c+2b)
2abc+4ab2c =2abc(1+2b)
https://youtu.be/ctqviXu-mTE
ALGEBRAIC FRACTIONS WITH MONOMIAL DENOMINATORS
Algebraic expressions are said to have monomial denominator if the denominator has a single term. Examples are xy,4a, b2, etc. However, algebraic fraction with monomial denominators is of the form: 4/y,5/3k,2/7x,…. To effectively simplify algebraic fractions, a good knowledge of LCM is
very necessary.
Examples:
Simplify the following:
1/3a+2/3a 2. d/7c+1/21c 3. (a-2b)/3+(a-3b)/5
Solutions:
1/3a+2/3a=(1+2)/3a=3/3a=1/a
d/7c+1/21c=(3d+1)/21c=(3d+1)/21c
(a-2b)/3+(a-3b)/5=(5(a-2b)+3(a-3b))/15=(5a-10b+3a-9b)/15=(8a-19b)/15
EVALUATION:
Simplify (x+y)/2-(x+3)/3
Simplify 2/3-(x-1)/x
Factorise 6a2b – 15ab2
Simplify 6x-3y-(4x-7y)
Expand (b-a)2

https://youtu.be/M1dGE0zGoZM
MISSING FACTORS IN ALGEBRAIC EXPRESSION
Examples:
Copy and complete the following:
18ts+9t=9(……..)
3bc+9abc=3c(…….)
25t-5r=5(…….)
Solutions:
18ts+9t=9t(2s+1)
3bc+9abc=3bc(1+3a)
25t-5r=5(5t-r)
EVALUATION:
Copy and complete the following:
pqs-2qs=qs(…….)
7rs-st=(…….)
4u+2ut=(2+t)
45vt-5vr=9(…….)
9xy-6xy=(3x…….)
https://youtu.be/I-4g550Q274
QUANTITATIVE REASONING ON ALGEBRAIC EXPRESSIONS

https://youtu.be/GmRixoQ5nC8